3.3 Двоично-десетичен суматор в код 2421
Тук
ще
разгледаме
тегловно
значимия код
2421, известен
още като код
на Емери,
който се дефинира
със следната
кодова
таблица:
Таблица 3.3.1.
Дефиниране
на код 2421
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0000 |
0001 |
0010 |
0011 |
0100 |
1011 |
1100 |
1101 |
1110 |
1111 |
Всички
останали
логически
комбинации (6
на брой),
освен горе
избраните, се
приемат за забранени.
Полезно е тук
да бъде
отбелязано, че
кодовите
комбинации
за цифрите от
първата
половина на
кодовата
таблица (0, 1, 2, 3 и 4),
интерпретирани
като двоични
числа, могат
да бъдат
изразени
така:
![]()
а
кодовите
комбинации
за цифрите от
втората
половина на
кодовата
таблица (5, 6, 7, 8 и 9),
интерпретирани
като двоични
числа, могат
да бъдат
изразени
така:
![]()
Кодът 2421
притежава
свойствата
четност, монотонност,
тегловна
значимост и
допълняемост.
Единственото
свойство,
което не
притежава, е
свойството
еднозначност.
Това налага
разглеждането
на останалите
6 възможни
двоични
комбинации
като
забранени.
Отпадналите
(забранените)
комбинации
са онези,
които не
изпълняват
свойството
допълняемост.
В светлината
на това
ограничение
обаче може да
се приеме, че
кодът 2421 е
максимално
близо до
изискванията
на
Рутисхаузер (вижте
книга [1]).
Освен това не
са известни
технически
решения за
аритметика
върху този
код, което
оправдава
вниманието
към него.
Реализацията
на всяка
аритметика
се основава
върху
техническата
реализацията
на операция
събиране,
чрез така наречения
суматор. Ето
защо
непосредствената
задача тук е
синтезът на
2/10-чен суматор
в код 2421.
Тъй като
кодът на
десетичните
цифри е двоичен,
решението се
търси въз
основа на
операция
събиране в
двоична
бройна
система, т.е. с
помощта на
двоичен
комбинационен
суматор. Като
се има
предвид още,
че десетичната
бройна
система е
позиционна, задачата
за събиране
на две
многоразрядни
числа се
свежда до
задача за
синтез на
едноразряден
2/10-чен суматор.
И така,
вниманието
се
съсредоточава
върху сумата
от две кодови
комбинации в
условията на
пренос от по-младшия
разряд:
![]()
Като се
има предвид,
че
двуместната
операция
събиране
трябва да се
подчинява на
комутативния
закон,
възможните
на брой
съчетания от
две кодови
комбинации
са:
![]()
Верността
на кодовата
сума следва
да се анализира
от гледна
точка на
правилата на
десетичната
бройна
система,
възможностите
на двоичната
бройна
система и
приетата по-горе
кодова
таблица.
Въпреки,
че кодовите
комбинации
не са двоични
числа, при получаване
на сумата (70), те
се
интерпретират
като такива,
защото
единственото
техническо
средство за
операция
събиране е
двоичният
суматор. В
смисъла на
тази
интерпретация,
забранените
комбинации
ще бъдат интерпретирани
като двоични
числа, както
е представено
тяхното
съответствие
в следната таблица:
Таблица 3.3.2 Забранени
комбинации
за код 2421
|
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
|
5 |
6 |
7 |
8 |
9 |
10 |
Следователно,
съответствието
на кодовата
сума на
забранена
комбинация,
може да се изрази
формално със
следното неравенство:
![]()
След
направения
анализ на
получаваните
двоични
кодови суми (70),
в условията
на събиране
без наличие
на пренос,
както и при
наличие на
пренос, се
констатира,
че не винаги
се получава
верен
резултат
(необходим
код на цифрата
на сумата ( d(z)i
). Всички
възможни
суми Si могат да
бъдат
класифицирани
в три групи:
a)
Суми,
които имат
вярно
съответствие
в смисъла на
кодовата
таблица;
b)
Суми,
които
представляват
забранени
комбинации,
но са в сила
неравенствата:
![]()
c)
Суми,
които
представляват
забранени
комбинации,
но са в сила
неравенствата:
![]()
В
случаите,
когато
получената
сума съответства
на забранена
комбинация,
тя трябва да
бъде
коригирана.
Корекцията
се търси като
двоично
число Ki, което след
събиране с
кодовата
сума Si, да
даде
правилен
десетичен
код за
цифрата zi и
правилен
десетичен
пренос pi. Тъй като
случаите, в
които се
налага
корекция са
два (втори и трети,
според
горната
класификация),
то общата
корекция Ki се
търси като дизюнкция
от вида:
![]()
Корекцията,
която следва
да се назначи
в условията
на случай b), не
трябва да
генерира
тетраден
пренос, тъй
като
десетичната
сума по
силата на (72), не
може да бъде
число
по-голямо от 9.
Тъй като
най-голямата
по стойност
забранена
комбинация е
10, то корекцията,
определена
като число,
което при
събиране с
кодовата
сума няма да
генерира
тетраден
пренос, е +6, т.е.
![]()
В
условията на
случай c), по
силата на
таблица 3.3.1,
кодовата
сума Si може да
бъде
изразена
както следва:
![]()
Тази
сума винаги
ще генерира
тетраден пренос,
който може да
се приеме за
необходимия десетичен
пренос ( piºp3 ), така
че в текущия
разряд
остава
разликата:
![]()
Тази
разлика, при
условията (73), може
да има за
минимална
стойност
числото 6,
което според
кодовата
таблица,
трябва да се
коригира
чрез
прибавяне на
неизвестна за
сега
константа,
т.е. така:
![]()
Като
имаме
предвид, че
комбинацията
от минималните
цифри, която
отговаря на
условие (73) е (5+5+0), може да се
определи, че
корекцията в
този случай
следва да
бъде числото:
![]()
Тъй
като
необходимият
пренос при
десетичното
събиране в
тези случаи
според (76) е
отчетен още
при първото
събиране, при
второто
събиране
според (77),
възможните
тетрадни
преноси не
следва да се
разпространяват.
В
резултат на
горе
изложения
анализ се стига
до
логическата
структура,
показана на фигура
3.3.1:
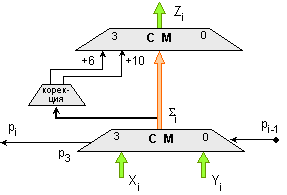
Фиг.
3.3.1. Логическа
структура на
суматор в код
2421
Единственият, все още неизяснен елемент в получената структура, е схемата за формиране на 2/10-чните корекции. Функциите на корекциите са две и техният аритметически анализ беше изложен по-горе. Логиката на анализа формира три необходими признака:
·
Признак
за забранена
комбинация,
който ще бъде
означен така:
FB (Forbidden);
·
Функция
за корекция +6,
означена C6 (Carry 6);
·
Функция
за корекция +10,
означена C10 (Carry 10).
Функциите
за корекция
зависят от
отношенията (72) и (73)
съответно,
ето защо са
необходими
две
логически
функции,
които да
разпознават
тези
ситуации. Тези
функции са
означени
така: DC4 за
разпознаване
на
отношенията (72) и DC5
за
разпознаване
на
отношенията (73).
Синтезът им
протича
върху
кодовата
таблица 3.3.1, на
която се
гледа като на
таблица за
истинност за
тези
отношения.
При това
положение
получаваме,
че:
![]()
където с x3 и y3
са означени
най-левите
битове в кодовите
комбинации
на двете
десетични цифри.
Функцията FB се синтезира върху таблица 3.3.2, на която се гледа като на таблица за истинност. След минимизация тя получава следния вид:
![]()
Окончателният
вид на
коригиращите
функции е
следният:
![]()
В
принципната
логическа
схема
функциите за
корекция се
превръщат в
числени
стойности,
аналогично
на 2/10-чните
корекции във
вече
разгледаните
суматори.
Принципната
логическа
схема на едноразрядния
2/10-чен суматор
е
представена
на фигура 3.3.2.
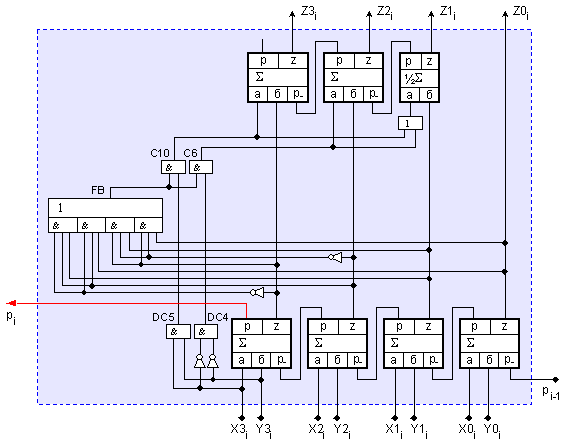
Фиг.
3.3.2. Принципна
логическа
схема на
суматора
Както
беше
изтъкнато в
глава 1 на книга
[1],
възможностите
за съставяне
на 2/10-чни кодови
таблици са
огромни и
по-точно 29,059,430,400.
Едва ли това
множество е
напълно
изследвано,
но ние
предлагаме
на Читателя
още един 2/10-чен
код – код 5211.
Какви са
неговите
свойства и
възможности
следва да
разберете
самостоятелно,
като се
възползвате
от
публикацията:
http://tyanev.com/resources/docs/BCD_Adder_in_a_weight_code-5211.pdf
Следващият
раздел е: