III.2.
Комбинационен
двоично-десетичен
суматор в код
с излишък +3
Двоично-десетичният
суматор за
събиране на
числа
представени
в кода с
излишък 3, т.е. (8421+3) също
се отнася към
тегловно
значимите
суматори.
Цифрите на
десетичните
операнди се
представят
чрез
4-разрядна
двоична комбинация
според
съответната
кодираща таблица
(вижте
книга [1]).
Когато
на кодовите
комбинации, с
които са кодирани
десетичните
цифри, се
гледа като на
цели двоични
числа, е
възможно
десетичната
сума Si в i-тия
разряд
![]()
да се
интерпретира
като двоична,
т.е. нейната
реализация
като
количество
става възможна
за
изразяване
(представяне)
в 4-битовия формат,
т.е. чрез
4-разряден
двоичен
суматор.
Според
кодиращата
таблица
обаче, на
входа на този
двоичен суматор
се подават
числата
![]()
т.е.
десетични
цифри,
представени
в кода с излишък
+3, което
означава, че
получената
двоична
сума Si ще
бъде в
същност
следната
![]()
която
очевидно не
съответства
по
количество
на търсената
десетична
сума.
Тъй като търсената десетична сума също трябва да се подчинява на кодиращата таблица, това означава, че сумата следва да бъде получена с излишък +3, т.е. така:
![]()
При
това
положение се
налага
изводът за принципно
невярната
двоична сума (според
уравнение (58)),
съдържаща 3
излишни
единици :
![]()
Ако
се
анализират
всички
двоични суми S,
които е
възможно да
получат на
изхода на
двоичния
суматор, се
вижда, че те
могат да се
разделят на
две групи - в
зависимост
от това дали
при
двоичното събиране
е възникнал
или не е
възникнал
тетраден
пренос. Ще
разгледаме
тези групи.
Първа
група се формира
от двоичните
суми, които не
предизвикват
тетраден
пренос и
следователно
това са суми,
които
удовлетворяват
следното
неравенство:
![]()
В
същност, това
са десетични
суми, не
по-големи от
числото 9,
което в кода
с излишък е
равно на
числото 12:
![]()
Ако
отчетем
принципната
грешка, с
която се получава
тази сума, се
вижда, че
вместо 12 се
получава 15,
което
отговаря на
посоченото
по-горе
неравенство.
От този
анализ се
разбира, че
сумите, за които
става дума,
не
предизвикват
десетичен
пренос и ако
трябва да се
получи
вярната сума,
следва да се
извърши
изваждането
![]()
Тази
допълнителна
операция се
нарича 2/10-чна
корекция.
Естествено
операцията
изваждане се
заменя с
операция
събиране в
допълнителен
код, която се
реализира с
втори
двоичен
суматор.
Събирането
на
междинната
сума
![]()
във
всички
случаи
предизвиква
двоичен пренос,
който според
теоремата за
събиране в допълнителен
код (вижте
в книга [1])
следва да не
се отчита в
резултата:
![]()
който по
количество
точно
съответства
на кодиращата
таблица.
Следва да
припомним, че
теглото на
тетрадния
пренос
(
p3 ) е 16
единици.
В
крайна
сметка,
коригирането
на сумата
след първото
двоично
събиране
изисква още
един суматор
и разпознаваща
логическа
функция за
суми от тази
група.
Очевидно е,
че това е
функцията:
![]()
Втора
група обединява
двоичните
суми, при
получаването
на които
възниква
тетрадният
пренос ( p3
). Това
означава, че
получаваните
при първото
двоично
събиране
суми
удовлетворяват
следното
неравенство
![]()
и не са
във
възможностите
на
4-разрядния
двоичен
суматор. Tази
ситуация съответства
на десетични
суми, които
надвишават
цифрата 9.
Обръщането
на посоката
на неравенството
за сумите от
втора група
означава, че
тук са всички
десетични
суми, които
генерират
десетичен
пренос, при
което веднага
може да се
установи
еквивалентността
на последния
с тетрадния,
т.е.
![]()
В
същото време
обаче, в
четирите
разряда на двоичната
сума остава
разликата
![]()
Тъй като десетте единици съответстват на необходимия десетичен пренос и ще бъдат отчетени в следващия разряд, то оставащият резултат в крайна сметка е разликата
![]()
Очевидно
е, че този
резултат не
е верен в
смисъла на
кодиращата
таблица и се
налага да се
коригира,
което може да
се осъществи
чрез прибавяне
на
недостигащите
му 3 единици.
Това може да
стане в
допълнителния
двоичен
суматор.
Разпознаващата
функция на
тази корекция
е
еквивалентна
на тетрадния
пренос, т.е.
![]()
Крайният
вид на
функцията за
корекция представлява
израза
![]()
Извършвайки
събирането
![]()
във
втория
двоичен
суматор, се
получава число,
което точно
съответства
на верния резултат,
според
кодиращата
таблица.
В
резултат на
изложения
анализ и
синтезирания
алгоритъм за
операция събиране се стига до
логическата
структура на
едноразрядния
2/10-чен суматор
в кода с
излишък 3, показана
на фигура III.3.
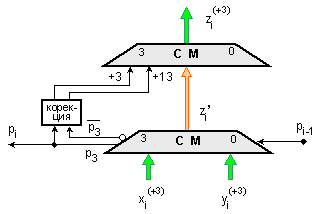
Фиг.
III.3.
Логическа
структура на
суматор в
кода 8421(+3)
В синтезираната тук логическа структура, 2/10-ните корекции са +3 и +13. Така в двоичния суматор на втория "етаж" се изпълнява едно от следните две събирания
![]()
Лесно може да се съобрази, че окончателната цифра в младшия разряд на резултантната тетрада z0 , е еквивалентна на инверсната стойност на младшия разряд, означен z0’ на входната сума от долния суматор:
![]()
а двоичният
пренос от
този разряд е
еквивалентен
на входната
цифра, т.е.
![]()
С
други думи,
4-разрядният
двоичен
суматор на
втория етаж
не съдържа
пълноценен
едноразряден
двоичен
суматор в
младшия си
разряд, а
само един логически инвертор.
След
отчитане на
всички
съждения относно
синтезираната
логическа
структура се
получава принципната
логическа
схема на
едноразрядния
2/10-чен суматор в код с
излишък 3,
представена
на фигура
III.4.
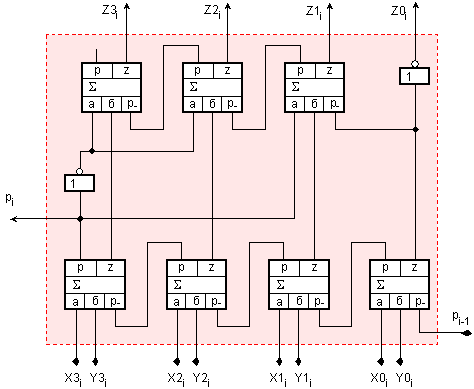
Фиг. III.4. Принципна
логическа
схема на
едноразряден
2/10-чен суматор
в кода 8421(+3)
Оценки и
изводи: Това
което може да
се каже, без
да се правят
някакви
изчисления е,
че
двоично-десетичните
суматори,
независимо в
какъв код на
десетичните
цифри ще
работят, са
значително по-сложни
от
комбинационните
двоични суматори.
Синтезираните
по-горе
логически схеми
представляват
едноразрядни
суматори.
Чрез тяхното
мултиплициране
може да се построи
2/10-чен суматор
с произволна
дължина с
последователен
пренос.
Въпросът за
повишаване на
неговото
бързодействие
следва да се
разглежда по
начина, вече
показан в
тази книга.
Натрупващи
2/10-чни
суматори
могат
най-лесно да
се построят
чрез подхода
на
разпределената
логика (виж
пункт II.5).
Числени
примери за
функционирането
на този
суматор са
представени
по-нататък в
тази книга
(вижте
съдържанието).
Въпроси
и задачи:
1.
Определете
времето за
превключване
на логическата
схема от
фигура III.4, като
укажете най-тежкия
случай.
2.
Реализирайте
едноразряден
2/10-чен суматор чрез
а)
ИС 7480;
б) ИС
7482;
в)
ИС 7483 и други
схеми с
по-висока
номенклатура
в серията.
3.
Предложете
подходи за
повишаване
на бързодействието
на схемата.
4.
Предложете
логическа
структура и
реализация
на 2/10-чен
едноразряден
суматор със
запомнена
таблица за
събиране в
ПЗУ.