III.
ДВОИЧНО-ДЕСЕТИЧНИ
СУМАТОРИ
III.1.
Комбинационен
двоично-десетичен
суматор в код
8421
Двоично-десетичният
суматор (2/10-См,
или още BCD-код) се
използува в
случаите,
когато
операндите
са представени
в
двоично-десетична
бройна система,
в която всяка
десетична
цифра на числото
се представя
(имитира) от
двоична
комбинация.
Въпросът за
кодирането
на десетичните
цифри и
свойствата
на
възможните
кодове са
разгледани в книга [1]. Когато
цифрите на тази
бройна
система се
кодират в
тегловно-значимия
код 8421 (код на
прякото
заместване),
това
означава, че
те се
представят
като цели 4-разрядни
двоични
числа според
съответната
кодираща
таблицата
(виж книга
[1]).
Структурирането
на суматора е
аналогично с
това на
двоичния, т.е.
задачата за
синтез на многоразрядния
2/10-чен суматор
се свежда до синтез
на
едноразряден
2/10-чен суматор,
в който се
осъществява
изчислението
на двете функции
- на
десетичната
сума от
съответните
десетични
цифри
![]() ,
,
и на
десетичния
пренос
pi.
Построяването
на
многоразрядни
2/10-чни суматори
на базата на
едноразрядния
се осъществява
по същия
начин, както
при двоичния,
например по
схемата с
последователен
пренос.
Синтезът на едноразряден 2/10-чен суматор в кода 8421 е свързан с три групи възможни десетични суми, които се разглеждат по-долу:
Първа
група: тази
група
включва суми S, удовлетворяващи
следното
неравенство:
![]()
например, 5+2=7 < 9, т.е.
суми, които
не
предизвикват
генериране на
десетичен
пренос от
текущия
разряд (pi=0).
Характерното
за тези суми
е, че ако
десетичните
цифри xi и yi се
интерпретират
като цели
4-разрядни
двоични
числа, а
преносът pi-1 като
двоична
цифра, защото
е пренос в
позиционна
бройна
система и
неговото тегло
в по-старшият
разряд е
равно на
най-малката
значеща
цифра, т.е. на
единица (1), то
резултатът
(сумата) се
получава без
двоично
препълване.
Получената
двоична сума
съответства
на такова
количество,
за което
според
кодиращата
таблица, има
определен
десетичен
символ. Това
означава, че
такива
двоични суми
са във
възможностите
на един
4-разряден
двоичен
суматор, т.е.
могат да се
получават
чрез него.
За съжаление съществуват десетични суми, които надвишават по количество цифрата 9. Такива суми има два вида и те се разглеждат отделно.
Втора
група: в тази група
се
обединяват
онези суми S, които
предизвикват
десетичен
пренос от текущия
разряд (pi=1), но
интерпретирани
като двоични,
те все още са
във
възможностите
на
4-разрядния
двоичен
суматор, в
който те се
получават,
т.е. не
предизвикват
двоичен
пренос.
Такива са
всички суми,
които
удовлетворяват
следното
неравенство
![]()
например, 5+8=13 < 15, но 13 > 10.
Според
определението
за събиране в
позиционна
бройна
система,
когато
разрядната сума
надвишава по
количество
основата на
бройната
система, в
текущия
разряд се
оставя разликата
от нея и
основата,
като се
разпространява
пренос. Тъй
като тук
обаче
4-разрядното
двоично
събиране не
предизвиква
пренос, то
получената
сума (z’i) (в
интервала [10¸15]) не е вярна
в смисъла на
кодиращата
таблица.
Следователно
този
резултат
трябва да се коригира.
Корекцията
трябва да
бъде такава,
че да се предизвика
десетичен
пренос и
останалия 4-разряден
код да
съответства
по количество
на
правилната
десетична
цифра според
кодиращата
таблица.
Най-малкото
число, което
може да се
предизвика
тетраден
двоичен
пренос за
суми от тази
група, е 6.
Следователно,
ако към
4-разрядната
двоична сума
се прибави
коригиращото
число 6, ще се
получи нова
двоична сума,
която се
намира в
интервала [16¸21]. Числата
от този
интервал
обаче не са
във възможностите
на
4-разрядния
двоичен
суматор и
следователно
при
събирането (z’i+6) ще
възникне
двоичен
пренос, чието
двоично
тегло е равно
на 16 единици.
Тези 16 единици,
с които се
ощетява оставащата
4-разрядна
двоична сума
отнасят в следващия
2/10-чен разряд
10-те единици
на желания в
случая
десетичен
пренос, плюс
още 6 единици,
с помощта на
които той е
предизвикан.
В крайна
сметка,
оставащият
4-разряден
резултат се
намира в
интервала
[10¸15] + 6 - (10 + 6) = [0¸5]
,
който точно съответства по количество на кодиращата таблица.
От синтезирания алгоритъм за събиране в тази група суми се вижда, че освен първото е необходимо и второ двоично събиране, което следва да се инициира при разпознаване на първичните двоични суми, включени в тази група.
Това
налага
включване на
втори
4-разряден двоичен
суматор и
синтез на
разпознаваща
функция,
която да
инициира
необходимата
корекция +6.
Задачата на
коригиращата
логическа
функция е да
разпознае
двоичните суми
в интервала [10¸15], ето защо
тя се
синтезира
като
дешифратор върху
съответстващите
двоични
комбинации. В
таблица III.1,
която
интерпретираме
като непълна
таблица на
истинност,
коригиращата
функция е
дефинирана
върху
подмножеството
“забранени”
комбинации.
Читателят не
бива да
забравя
дуалността,
която
осигурява
двоичната
бройна система.
Тя ни
позволява да
интерпретираме
в случая
двоичната
сума
![]()
като логическа комбинация и така да синтезираме логическа функция.
Таблица
III.1
|
|
|
|
|
K |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Картата на Карно ни позволява да получим МДФ на функцията:
|
|
|
|
|
|
|
|
|
|
00 |
01 |
11 |
10 |
|
|
00 |
0 |
0 |
0 |
0 |
|
|
01 |
0 |
0 |
0 |
0 |
|
|
11 |
1 |
1 |
1 |
1 |
|
|
10 |
0 |
0 |
1 |
1 |
![]()
Тъй като този вид на коригиращата функция е получен от анализа само на втората група суми, то тя носи съответния индекс, а полученият логически израз се счита все още за неокончателен.
Трета
група: в тази
последна
група се
отнасят
всички десетични
суми S, които
надхвърлят
числото 15,
![]()
например, 9+8=17 > 16. Най-голямата
възможна
сума е 9+9+пренос=19.
Тези
десетични
суми,
аналогично
на сумите от
предидущата
група, се
представят
чрез
десетичната
разлика от
основата на
бройната
система като
същевременно
разпространяват
десетичен
пренос pi.
Разгледани
обаче и
получени
като двоични,
те се
характеризират
с това, че не
са представими
с 4 двоични
разряда, т.е.
не са във
възможностите
на
4-разрядния
двоичен
суматор, чрез
който могат
да се получат
и
предизвикват
тетраден
пренос.
Тетрадният
пренос има
тегло 16
единици.
Следователно
оставащата
4-разрядна
двоична сума (z’i) е
ощетена с 16
единици, т.е.
![]()
Ако
горната
разлика се
интерпретира
като десетична,
то се вижда,
че
тетрадният
пренос
ощетява
десетичния
резултат с
още 6 единици,
така че след
първото
двоично
събиране, получената
двоична сума (z’i) не е
вярна. Тя
може да стане
вярна, ако се коригира
чрез
добавяне на
липсващите й
6 единици.
Това налага
включване на
втори двоичен
суматор,
както и
синтез на
разпознаваща
функция,
инициираща
корекцията +6.
Лесно може да
се направи
изводът, че
коригиращата
функция
(разбирана
като
логическа) в
този случай
тук е
еквивалентна
на тетрадния
пренос:
![]()
В
резултат на
изложения
теоретичен
анализ се
стига до
логическата
структура на
едноразрядния
2/10-чен суматор,
показана на
фигура III.1.
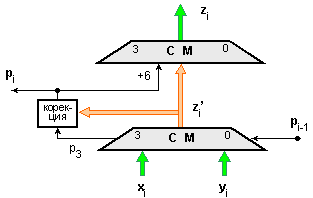
Фиг.
III.1. Логическа
структура на
суматор в
кода 8421
Тъй като корекцията по тегло има само две стойности - 0 или +6, то те могат да се интерпретират чрез логическите стойности на нейното логическо уравнение, което има вида:
![]()
Като
се има
предвид
фактът, че
стойността
на
коригиращата
функция K е
равна на
единица
винаги,
когато е
необходимо
да се
разпространи
десетичен
пренос, става
очевидно, че
![]()
Тази
еквивалентност обяснява
двоякото й
интерпретиране
- и като
десетичен
пренос, и
като 2/10-чна
корекция 0
или 6.
Една
примерна
реализация
на
синтезираната
логическа
структура
представлява
представената
на фигура III.2
принципна
логическа
схема.
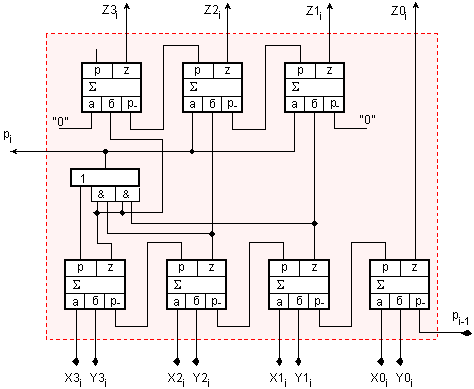
Фиг. III.2. Принципна
логическа
схема на
едноразряден
2/10-чен суматор
в кода 8421
Единственото
обяснение,
което
изисква тази
логическа
схема е за
липсата на
едноразряден
двоичен
суматор в
младшия
разряд на втория
"етаж". Тази
липса се
обяснява с
факта, че
младшата
двоична
цифра и на
двете корекции
(+0,+6) е винаги
нула (0), т.е.
фактическото
събиране в
младшия разряд
на втория
етаж е (![]() ) винаги и
то не изисква
двоичен
суматор.
) винаги и
то не изисква
двоичен
суматор.
Числени
примери за
функционирането
на този
суматор са
представени
по-нататък в
тази книга
(вижте
съдържанието).
Въпроси и
задачи:
1.
Определете
времето за
превключване
на логическата
схема от
фигура III.2 като
укажете най-тежкия
случай.
2.
Реализирайте
едноразряден
2/10-чен суматор чрез
а) ИС 7480;
б) ИС 7482;
в) ИС 7483 и
други схеми с
по-висока
номенклатура
в серията.
3.
Предложете
подходи за
повишаване
на бързодействието
на схемата.
Анализирайте
възможностите
за
повишаване
на
бързодействието
на
многоразрядния
2/10-чен суматор
по аналогия с
двоичния
суматор.
Следващият
раздел е:
3.2
Комбинационен
двоично-десетичен
суматор с
излишък (+3)