3.3.1
Операция
събиране и
операция
изваждане на
числа с ПЗ
Operation addition and subtraction
Тези
две операции (Z=X+Y,
Z=X-Y) ще
бъдат
разгледани
съвместно,
тъй като при
числа със
знак те се
свеждат
алгоритмично
практически
към една
операция - събиране.
Целта ни ще
бъде не
просто да
обясним машинните
алгоритми за
изпълнение
на тези операции,
а да ги
изясним, излагайки
техния
синтез.
Резултатът
от тези
операции се
изразява по
следния
начин:
![]()
В
получения
израз се
съдържа
операция умножение,
която е
по-приоритетна от
основната и
изисква
приложението
на
дистрибутивния
закон, според
който
мащабният
коефициент
може да бъде
изнесен пред
или зад
скоби. Ще
припомним, че в горния
запис с q е
означена
основата на
бройната
система и че
за двоичната
тя е q=2.
За съжаление,
в общия
случай
порядъците
на
операндите
са различни и
възниква
въпросът: Кой
мащабен
коефициент
да бъде
изнесен зад
скоби? От
математическа
гледна точка
въпросът е
несъстоятелен,
но от гледна
точка на
практическата
реализация той
е от
изключителна
важност,
което и ще
докажем по-долу.
Ако
предположим,
че за
порядъците е
изпълнено
съотношението
![]()
и изнесем зад скоби мащабния коефициент на първия операнд, ще получим следния израз:
![]()
Според
този израз,
преди да се
извърши
основната
операция
събиране
(изваждане),
трябва да се
извърши
операцията
умножение на
мантисата My с
новополучения
мащабен
коефициент
![]()
Вече
беше
пояснено, че
това
умножение се
заменя с
изместване,
дължащо се на
специалния
вид на
множителя.
Мантисата My трябва
да се измести
относно
фиксираната запетая
на толкова
разряда,
колкото е
модулът на
разликата от
порядъците.
Посоката на
изместване
се определя
от знака на
същата
разлика. При
приетото в
случая
съотношение
на
порядъците
следва, че
разликата
![]()
ще бъде
положително
число, което
означава, че
изпълнявайки
умножението,
мантисата My трябва
да се
измества наляво.
Изместването
наляво обаче
е крайно
опасно поради
факта, че
мантисата се
намира в поле
с ляво
фиксирана
запетая.
Всяко
изместване
наляво
означава
загуба на старши
значещи
цифри от
мантисата My, което
естествено е
недопустимо.
Ето защо за
практическата
реализация
на операция събиране
не
е без
значение
кой от
мащабните
коефициенти
в израза (3.3.1.1) ще
бъде изнесен
зад скоби.
Във всички
случаи за
предпочитане
е да бъде
изнесен онзи
мащабен
коефициент,
който
съответствува
на по-големия
порядък. В
този случай
разликата на
порядъците,
която
неизбежно ще
трябва да се
получи, ще
бъде гарантирано
отрицателна.
Това пък от
своя страна
означава, че
мантисата,
която ще се
денормализира,
ще се измества
винаги и
само надясно.
Изместването
надясно е за
предпочитане,
тъй като при
него
евентуално
от мантисата
ще отпадат
младши цифри
и
следователно
загубата на
точност ще
бъде
значително
по-малка. Има
се предвид
крайната
дължина на
полето, в
което се
съдържа
мантисата.
При
изместване
на съдържанието
съответните
крайни цифри
излизат
извън
границите на
това поле и в
този смисъл
се говори, че
те се губят.
След
тези
съждения
изпълнението
на операция
събиране
(изваждане)
може да се
изрази така:
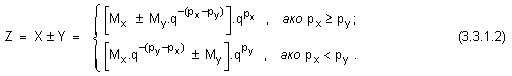
От
така
получения
математически
запис може да
бъде
представен
следващият
по-долу най-общ
вид на
алгоритъма
за
изпълнение
на операция
събиране
(изваждане),
който
представлява
последователност
от 5 основни
етапа. И тук, както
във формата с
фиксирана
запетая, при
машинното
изпълнение
на
операциите, освен
резултат
следва да се
получат и
признаците
на резултата.
Тъй като
алгоритмите на
аритметическите
операции върху
числа,
представени
във форма с
плаваща
запетая, са
значително
по-сложни от
тези във
форма с
фиксирана
запетая, то
между тях не
може да се
открие
обикновенна
аналогия. Всичко
това налага
многократно,
многослойно
и
многостранно
разглеждане
на всеки един
етап на
отделните
алгоритми,
ето защо към
най-общото
представяне
на
алгоритъма
за събиране,
което следва
по-долу, ще се
връщаме в
обясненията
си
многократно.
Нещо повече, тук
в хода на
изложението
на
алгоритмите,
ще бъдат
разяснени
допълнителни
понятия и свойства
на
разглежданата
форма за
представяне
на числата.
Ще бъдат
допълнително
обосновани
отделните
решения за
организация
на
разрядната
мрежа,
представена
в глава 1,
което не беше
подходящо да
бъде направено
там
(пункт 1.1.6.2).
И
така,
алгоритъмът
е последователност
от следните
общи етапи:
1.
Проверка на
значенията
на мантисите.
Ако
мантисата на
втория
операнд My=0, то за
резултат се
приема
първият
операнд: Z=X.
Ако
мантисата на
първия
операнд Mx=0, то за
резултат се
приема:
·
При
събиране - вторият операнд Z=Y ;
·
При
изваждане - Z=-Y .
Тази
проверка е
уместна, като
се има предвид
видът на
машинната
нула (1.1.6.2.16).
2. Сравнение
на
порядъците.
За да се
направи
необходимият
според формула
(3.3.1.2) избор, порядъците
px и py се
сравняват.
Необходимо е
да се
определи кой
от тях е
по-големият. За
целта се
получава
разликата (px-py). Ако
разликата
между
порядъците е
толкова голяма,
че числата се
оказват
несравними,
т.е. ако
![]()
където с m
традиционно
е означена
дължината на
подполето от
разрядната
мрежа, в
което се
представя мантисата
(вижте фигура
1.1.6.2.2), то за
резултат се приема
операндът с
по-големия
порядък. Например:
·
Ако (px-py)>0, то Z=X ,
·
Ако (px-py)<0, то Z=Y при
събиране и Z=-Y
при
изваждане.
Ако
порядъците
са равни, т.е.
ако (px-py)=0, то
следващият
трети етап,
се прескача.
3. Изравняване
на
порядъците.
Изравняване
на
порядъците
се извършва
чрез
изместване
на мантисата
надясно на
онзи операнд,
който има
по-малък
порядък.
Изместването
се извършва,
докато
разликата (px-py) се
нулира, т.е.
докато се
постигне
равенството (px=py), както
изисква (3.3.1.2).
4. Събиране
на мантисите.
Извършва
се събиране
(изваждане)
на така подготвените
мантиси на
двата
операнда. Това
става с
използване
на
допълнителен
код. Получената
сума е
предварителната,
т.е. не
окончателната
стойност на
мантисата на
резултата. В
получения
вид обаче
тази мантиса
не може да
остане, тъй
като
най-вероятно
тя не е
нормализирана,
т.е. не
отговаря на
условието (1.1.6.2.2).
Следователно
следва още
един етап.
5. Нормализация
на резултата.
Ако
получената
сума, която
трябва да
съответства
на Mz, е
нула, то
нормализацията
е невъзможна.
Тогава за
резултат се
приема
машинната
нула, имаща
вида (1.1.6.2.16). В
зависимост
от машинния
код,
използван за
представяне
на мантисата,
машинната
нула може да
бъде със знак
или без знак.
Получената
мантиса може
да бъде
ненормализирана
както
отдясно, така
и отляво. В
първия
случай
мантисата се
получава с
препълване,
което я прави
число
по-голямо от
единица.
Такава
мантиса се
нормализира
с
едноразрядно
модифицирано
аритметическо
изместване надясно
(вижте
пункт 3.2.3), като
при това
порядъкът се
увеличава с
единица.
Във
втория
случай
степента на
ненормализацията
отляво може
да бъде много
по-голяма от
един разряд (един
порядък).
Трябва да
припомним, че
тази степен
се измерва с
така
нареченото "ниво
на недостиг". В
този случай
мантисата се
нормализира,
като се
измества
наляво
последователно
на един
разряд,
докато се
изпълни
условието (1.1.6.2.2), като при
всяко
изместване
от порядъка се
изважда
единица.
Всеки от
етапите на
описания
алгоритъм заслужава
специален
коментар.
Така например,
уместността
на първия
етап се
обосновава
от избрания
за машинната
нула вид. Мотивите
за този вид
се състоят в
следното:
ако се
приеме, че
едно число,
което е равно
на нула, във
форма с
плаваща запетая
се представя
с порядък p,
различен от pmin, то при
събиране на
това число с
друго число,
което има
по-малък
порядък от
този на първото
и мантиса,
която е
различна от
нула, същата
би могла да
изчезне в
процеса на
изравняване
на
порядъците,
ако разликата
между тях е
достатъчно
голяма.
Очевидно
резултатът
от
операцията в
такава ситуация
ще бъде също
число равно
на нула. Този
резултат Z=0 се
характеризира
с голяма
загуба на
точност, тъй
като сумата Z=0+Y
се получава
равна на нула
въпреки, че Y0.
Ето защо
числото нула
следва да се
представя
във форма с
плаваща
запетая не с
какъв и да е
порядък.
Приемането
на минимално
възможната
стойност pmin за
порядък на
машинната
нула ще
доведе при операция
събиране (0+Y) на
втория етап
от
алгоритъма
до установяване
на
отношението pmin<py; на
третия етап
ще доведе до
изравняване
на pmin
към py; а
на четвъртия
етап - до
събирането (0+My):
![]()
В
крайна
сметка
резултатът
ще бъде
![]()
т.е. той ще
бъде получен
без загуба на
точност!
По
време на втория
етап се
проверява
дали
разликата в
порядъците не
надхвърля по
абсолютна
стойност
числото (m-1), което
представлява
дължината на
значещата
част от
полето на
мантисата (виж фиг. 1.1.6.2.2). Ако
разликата е
наистина
по-голяма от
това число,
то
следващият
етап е
безсмислен,
тъй като при
изравняване
на по-малкия
порядък към
по-големия,
изместващата
се надясно мантиса,
ще се окаже
извън полето,
в което първоначално
е била, т.е. тя ще
изчезне. В
резултат на
изчезване на
мантисата на
числото с
по-малкия
порядък,
операцията
(събиране,
изваждане) се
обезсмисля, ето
защо в този
случай
алгоритъмът
завършва на
втория етап,
с един от
следните
резултати:
·
При
събиране Z=X,
или Z=Y ;
·
При
изваждане Z=X, или Z=-Y.
Според
смисъла на
казаното в
глава 1, в описания
случай става
дума за
операнди,
които се
намират
върху
числовата ос
в твърде отдалечени
зони, в
резултат на
което
по-малкото число
се оказва
по-малко от
дискрета d
на зоната
(изразен чрез
(1.1.6.2.5)), в която се
намира
по-голямото
число. Този
резултат се
характеризира
със загуба на
значещата
част на
числото с
по-малкия
порядък, ето
защо тази
ситуация се
нарича "загуба
на
значимост".
Третият
етап в
алгоритъма е
свързан с
процедурата
за изравняване
на
порядъците.
Тя се
изпълнява само
в случай, че
абсолютната
стойност на разликата
на
порядъците
не надхвърля
числото (m-1), т.е. когато
![]()
Ако това
отношение е
изпълнено,
започва изместване
надясно на
онази
мантиса,
чийто порядък
е по-малък - според (3.3.1.2)
това е
мантисата My в първия
случай и
мантисата Mx във
втория
случай.
По-големият
от двата порядъка
се съхранява
в качеството
му на предварителна
и
неокончателна
стойност на
порядъка на
резултата.
Тази
стойност не е
окончателна,
защото тя
може да
претърпи
изменения в
резултат на
редица
ситуации,
които са възможни
по време на
следващите
етапи.
По
време на
изравняването
на
порядъците, изместващата
се надясно
мантиса
загубва толкова на брой
младши цифри,
колкото е
разликата
между
порядъците.
Ако
порядъците
са различни,
каквито са
най-често
реалните
ситуации,
загубата на
младши цифри
е неизбежна,
ето защо тази
грешка в
стойността
на денормализиращата
се мантиса,
също се
определя като
принципна.
Тя може да
бъде
намалена
единствено
чрез
представяне
на резултата
в разширен
формат, ако
такъв е
възможен за
разрядната
мрежа.
Принципните
грешки не
могат да бъдат
избегнати.
Споменатата
токущо грешка
е втора по
ред, след
описаната в
глава 1 грешка,
свързана с
неточното
преобразуване
в двоична
бройна
система на
числата с
ляво фиксирана
запетая. Ето
защо
процедурата
за
изравняване
на порядъците
се счита за
основен
източник на грешка
в крайния
резултат.
Очевидно
максималната
относителна
погрешност
на сумата
(разликата)
се оценява с
израза (1.1.6.2.11) и
реално се
намира в
интервала (1.1.6.2.12).
Четвъртият
етап, в
който се
извършва
събирането
на вече подготвените
в предидущия
етап мантиси,
не се нуждае
от специален
коментар, тъй
като проблемите
на операция
събиране
(изваждане) на
числа с фиксирана
запетая вече
бяха
изяснени. Все
пак трябва да
бъде
отбелязано,
че е вероятно
настъпване
на препълване
в полето на
мантисата
при
получаване
на резултата.
Този факт обаче
няма
съществено
значение,
предвид на разглежданата
форма за
представяне
на числата.
Практически
препълването
в полето на
мантисата
може да бъде
отстранено,
както вече
беше
пояснено, в
следващия,
пети етап на
алгоритъма.
Тъй като
мантисите са
числа със
знак,
операцията
се извършва в
допълнителен
код.
Резултатът
обаче следва
окончателно
да се
представи в
прав код.
В
последният пети
етап, се
проверява
дали
получената
сума (разлика)
е
нормализирано
число. Ако
числото е
нормализирано,
то се приема
за мантиса на
резултата.
Веднага
трябва да
отбележим, че
разпознаването
на
нормализирания
вид на
мантисата е
проблем,
който е
напълно аналогичен
на
разгледания
в пункт 3.2.8 при
операция
деление.
Следователно
тук е напълно
приложима
синтезираната
там
логическа функция
за
разпознаване
на лявата
нормализация
(3.2.8.5),
естествено
при отчитане
на разрядността
и
положението
на мантисата
в структурата
на
разрядната
мрежа. Това
се дължи на
факта, че
алгебрическата
сума в полето
на мантисата
се получава в
допълнителен
код.
Получената
сума
(разлика) е
възможно да
бъде много
малко число,
в частност
дори точна
нула. Като
имаме
предвид
форматите на
разрядната
мрежа с
плаваща
запетая,
както и
понятието
ниво на
недостиг,
читателят
следва да разбира,
че този
напълно
възможен
силно денормализиран
резултат
също може да
загуби своето
значение и да
бъде
възприет като
числото
машинна нула.
Процедурата
за нормализация
на такава
мантиса е
ненужно да се
изпънява и
приемайки за
резултат
машинната
нула,
практически
и в този етап
се реализира
ситуацията “загуба
на значимост”.
Ако
получената
сума е с
препълване,
то тя е ненормализирано
число
отдясно, т.е.
![]()
Този
резултат се
нормализира
(както вече беше
пояснено)
чрез
Модифицирано
аритметическо
изместване
надясно на
един бит,
което е
съпроводено
с корекция на
предварителната
стойност на
порядъка.
Изместването
надясно на
мантисата е
съпроводено
със згуба на
нейна младша
цифра. Това е
принципна и
неотстранима
грешка.
Корекцията
на пораядъка
се състои в
прибавяне на
единица, при
което, ако
предварителната
му стойност е
положително
число,
съществува
вероятност
от положително
препълване
в полето на
порядъка.
Както вече
беше пояснено
в глава 1, в
този случай
операция
събиране
(изваждане)
на числа с
плаваща
запетая следва
да завърши с
непредставим
в разрядната
мрежа
резултат,
който се
сигнализира
с генериране
на признака
за "препълване
при плаваща
запетая".
Като се
вземе под
внимание
диапазонът
на порядъка
на
представимите
числа, който
се определя
според
зависимостта
(1.1.6.2.21), горе
описаната
ситуация на
препълване
при плаваща
запетая
довежда
фактически
до резултат,
който според таблица 1.1.6.2.2 се
характеризира
като безкрайност
или като NAN, т.е. "не е
число". В
зависимост
от знака на
резултата,
може да имаме
положителна
или
отрицателна
безкрайност
или +NAN и -NAN. С
получаване
на този
резултат и
формиране на неговите
признаци
операцията
завършва.
Естествено,
участие на
този неверен
резултат в
по-нататъшните
изчисления
не бива да бъде
допускано,
което
разбира се е
отговорност
на
програмиста.
Ако
получената
сума в полето
на мантисата е
ненормализирано
число отляво
(споменахме
за тази
възможност
малко по-горе),
с ниво на
недостиг r, то нормализацията
на това число
е процес на
последователно
изместване
наляво с
корекция на
порядъка (-1) на
всеки разряд.
Очевидно при
указаното ниво
на недостиг r, в младшата
част на вече
нормализираната
мантиса ще се
установят r на брой
незначещи
нули, а от
предварителната
стойност на
порядъка ще
бъдат
извадени r
единици. Ако
обаче преди
нормализацията
тази
стойност на
порядъка е
била
отрицателно
число, на
определен
етап от
неговата
корекция,
например
след f
на брой
измествания
наляво, т.е.
след изваждане
на f
единици, е
възможно в
полето на
порядъка да
настъпи
отрицателно
препълване,
т.е. да се получи
число, което
е по-малко
от най-малкия
представим
порядък.
Формално
този случай
удовлетворява
следното
отношение:
![]()
Тази
ситуация
(отрицателно
препълване в
полето на
порядъка) се
нарича "изчезване
на порядъка"
или антипрепълване. Практически
(ако
изчезването
на порядъка е
настъпило
преди да бъде
нормализирана
мантисата) се
получава
число, което
върху
числовата ос
стои по-близо
до числото
нула, ето
защо в този
случай за
резултат
най-често се
приема машинната
нула. Това
изисква
алгоритъмът да
завърши с
изчистване
на
съдържанието
на полето на
мантисата и
установяване
на pmin в
полето на
порядъка.
Това обаче не
е единствената
възможност. В
съвременните
процесори за
работа с
плаваща
запетая
съществува
възможност
резултатът с
ненормализирана
мантиса да
продължи да
участвува в
този си вид в
следващите
изчисления, в
които той има
възможност
да влезе с [(m-1)-(r-f)]
на брой верни
цифри в
полето на
мантисата. В
посочения
току-що
израз,
величината f
представлява
изместванията
на мантисата
наляво, т.е.
броят на
единиците, с
които се снижава
нивото на
недостиг r, (f<r).
Възможността
да се работи
и с
ненормализирани
числа позволява
да бъде
намалена
абсолютната
погрешност в
изчисленията.
В
заключение
трябва да се
отбележи, че
последният
пети етап е
също
източник на
грешки, които
се дължат
отново на
загуба на
младши цифри
от
изместващата
се мантиса.
Тези грешки
са също принципни,
те не могат
да бъдат
отстранени,
но могат да
бъдат
намалени
чрез
използването
на по-дългите
формати.
Особеностите
на
аритметиката
с недостиг ще
бъдат
пояснени
по-късно.
Първите
два етапа на
алгоритъма
за събиране,
които бяха
коментирани
по-горе,
дават основание
да се въведе
една
специфична
оценка на
устройствата
за работа с
плаваща запетая,
която се
нарича "машинно
епсилон".
Машинното
епсилон e
или още
машинната
точност, може
да бъде оценена
чрез
операция
събиране по
следния
начин:
e = q (3.3.1.3)
където q е
минималното
число с
плаваща
запетая, за което
след
изпълнение
на операция
събиране, все
още е в сила
неравенството
1 + q > 1 .
(3.3.1.4)
В
редица потребителски
програми
числото e се
използва
като основа
за оценка на
точността на
изчисленията.
В случаите,
когато една и
съща
потребителска
програма
трябва да се
изпълнява в
различни
процесори,
нейната
зависимост
от машинното
епсилон на
същите може
да се адаптира
автоматично.
За целта
трябва да се
започне с
изчисляване
на числото e,
което може да
се осъществи
със следния
алгоритъм,
реализиращ
зависимостта
(3.3.1.4):
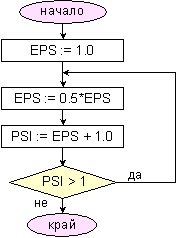
Фиг. 3.3.1.1. Алгоритъм
за
изчислявана
на машинното
епсилон EPS
Представената
блок-схема
представя
един цикъл от
вида с
предварително
неизвестен
брой
повторения, в
който условието
за край е
неравенството
(3.3.1.4). На излизане
от този
цикъл,
променливата
EPS
съдържа една
оценка на
машинната
точност. Програмната
реализация
на този
алгоритъм
изисква
променливите
да бъдат
декларирани
от
съответния тип,
чиято
машинна
точност ще
бъде
определяна.
Например тип Real , формат Double
precision.
Според (1.1.6.2.11), при q=2 и m=24[b], т.е. за
най-често
използвания
формат на числата
с плаваща
запетая,
величината e се
оценява с
еквивалентната
в десетична бройна
система
стойност
![]()
Вмъкването
на подобен
фрагмент в
потребителските
програми и
използуването
на получената
оценка за
машинната
точност EPS в съответния
алгоритъм ги
прави
машинно
независими. В
някои
програмни
езици има
фотови функции
за
определяне
на машнната
точност.
В
областта на
програмирането
битува още един
термин - "катастрофално
взаимно
унищожение".
Ситуацията
наречена с
това
екзотично
наименование
е свързана с
операция
изваждане.
Типичен
пример за
тази
ситуация са
програми, реализиращи
циклически
алгоритми от
вида с
предварително
неизвестен
брой повторения,
в които
най-често
като условие
за край на
цикъла се
използва
някакво
неравенство
от вида
![]()
изразяващо
сходимостта
на
съответния
числен метод,
чрез
величината А.
Програмистът
е длъжен да
отдели
специално
внимание на
условието за
край на
циклическите
изчисления,
тъй като е
известно, че
процесът на
схождане
може да бъде
както
апериодичен
така и
периодичен.
В случая
операция
изваждане на
двете последователни
итерационни
стойности
![]()
е
необходима
за да се
установи
абсолютната
разлика
между
старата и
новата
стойност на
сходящата
величина А. Ако
численият
метод е
наистина
сходящ, тази
абсолютна
разлика ще
клони към
нула. Обаче
операция
изваждане може
да ви поднесе
невероятни
резултати. Например,
ако
![]()
то:
![]()
Ето защо
на машинното
епсилон
трябва да се гледа
като на оценка
на относителната
погрешност,
с която се
изпълнява
операция
събиране (изваждане),
което ще
предпази
програмиста
от описаната
по-горе
заблуда и
неправилно
съставяне на
условието за
край на
цикъла. По същество
обаче
операция
изваждане се
извършва
правилно.
Ако се приеме,
че числото X
се представя
във форма с
плаваща
запетая неточно,
със загуба на
част
от значещата
му част
(вижте фигура
1.1.6.2.1), то
връзката
между
точната
стойност X и
изображението
XПЗ, е
следната:
![]()
откъдето
величината d,
представяща
неточността
на
изобразяване,
се определя с
отношението
![]()
и се
нарича относителна
грешка.
И
така, в
системите с
плаваща
запетая,
операциите
събиране и
изваждане на
почти равни величини
могат да
доведат до
значително увеличение
на относителната
грешка в
сравнение с
възможностите
на
разрядната
мрежа.
Например, ако
за изобразяване
на мантисата
са приети 5 десетични
разряда, т.е.
![]()
резултатите
от операция
изваждане на
числата
![]()
ще
коментираме
така:
![]()
Тук
функцията FLOAT
изразява
действията в
алгоритъма
за работа с
плаваща
запетая и
съответния
резултат
получен от
него.
Получената
стойност се
различава от
истинската
стойност
![]()
с
абсолютната
грешка:
![]()
Изчислението
на разликата FLOAT(X-Y) в случая е
извършено с
относителната
погрешност
![]()
която
е над 500 пъти
по-голяма от e. С други
думи, само
една от
десетичните
цифри в
мантисата на
резултата е
вярна.
Причината за
толкова
ниската
точност, или
още за
толкова
малко верни
цифри в мантисата
на резултата,
е загубата на
значещи
цифри от
мантисата на
умалителя в
процеса на
изравняване
на
порядъците.
Както вече
беше
посочено при
коментара на
третия етап
от
алгоритъма,
това е
принципна
грешка, която
може да се
намали чрез
използване
на разширени
формати. След
нормализация
на резултата,
същият може
да се
представи
отново в
по-късия
формат при
пълна
гаранция за
верността на
всички цифри
в мантисата.
Едно
от
следствията,
резултат от
описания алгоритъм
за операция
събиране
(изваждане),
представлява
нарушението
на
асоциативния
закон :
FLOAT [ FLOAT(a+b) + c] FLOAT [a + FLOAT(b+c) ] (3.3.1.7)
за някои
стойности на a, b и c.
Например, за
двете страни
на горното
отношение, се
получава:
(
11111113,0 - 11111111,0 ) + 7,5111111 = 9,5111111 ;
11111113,0 + ( -11111111,0 + 7,5111111 ) = 10,000000 ,
т.е.
разликата
между двата
резултата е
почти
половин
единица!
Математическото означение на регулярна сума:
![]()
по своята
същност е
основано на
предположението,
че е в сила
асоциативният
закон. Ето
защо,
натрупвайки
подобни суми,
програмистът
е длъжен да
бъде
особенно
бдителен за това,
дали в
процеса на
натрупване
![]()
не се нарушава
асоциативният
закон, с
което точността
може да се
влоши грубо.
Особено
полезно е да
подчертаем
тук, че
работата по
синтез на
най-правилния
алгоритъм е
изключително
творческа и
отговорна. Не
винаги
най-удобният
за
програмиране
алгоритъм е
най-добрият!
Ето защо
търсенето и
сравнението
на различни
алгоритмични
схеми за
натрупване,
ще доведе до
правилния
избор. За
дадения
по-горе
пример ще си
позволим да
предложим
например
следната
пирамидална
схема:
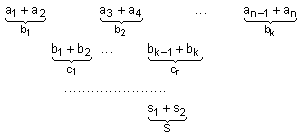
Предложената
алгоритмична
схема се
характеризира
с това, че тя отстранява
натрупването
на повече от
два елемента,
което се
постига за
сметка на
допълнително
въведените
множества
междинни
(временни)
суми. За
същността на
натрупването
четете книга [2].
Както вече споменахме, отговорността за точността на изчисленията се носи от програмиста, тъй като той избира или синтезира алгоритмите. Това той прави като изхожда от всичко, което му е известно за цифровия процесор от една страна и за конкретното поведение на данните от друга страна.
Въпреки, че при събиране асоциативният закон не винаги е в сила, то комутативният трябва да бъде винаги в сила, т.е.
FLOAT(a+b) = FLOAT(b+a) (3.3.1.8)
В сила са още следните закони:
FLOAT(a-b) = FLOAT [a+(-b)] , (3.3.1.9)
-FLOAT(a+b) = FLOAT [(-a) + (-b)] , (3.3.1.10)
FLOAT(a-b) = -FLOAT(b-a) . (3.3.1.11)
Функцията FLOAT(a+b) = 0 тогава и
само тогава,
когато
![]()
Като
имаме
предвид вече
казаното за
машинната
нула, то
![]()
Тези
закони не
биха били в
сила, ако в
системата с
плаваща
запетая, за
дробната мантиса
вместо прав
код, се
използуваше
допълнителен
код. Ето
защо при
представяне
на числата
във форма с
плаваща
запетая правият
код има
определено
теоретично
предимство
пред
допълнителния
код!
Често
при
програмиране
на сложни
математически
изчисления
се налага да
се въведе функция,
изразяваща
степента на
точност чрез
правилото за
закръгляване.
Тази функция
се означава round(X,v) и
изразява
стойността
на Х след
закръгление
до v разряда в
значещата
част на
числото и
математически
се определя
по следния
начин:
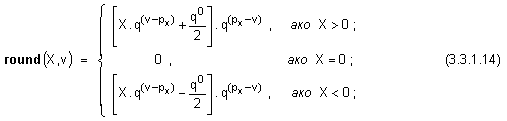
където Х е
реално число;
px е
порядъкът на FLOAT(X) с
нормализирана
мантиса, а v е цяло
положително
число, което
преставлява броя
на
оставащите в
значещата
част на
числото
цифри. С други думи
означението FLOAT(X) изразява
числото X със значещата
част,
представена
само от старшите
v
цифри, както
е показано на
следващата
рисунка:
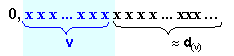
Непредставената
значеща част
на числото по
отношение на
представената
може да има тегло
равно
максимум на
стойността
на дискрета
за зона с
порядък v, означен в
рисунката с d(v). Както се
вижда от
определението
за функцията round,
закръглянето
се постига
чрез
операция
събиране с една
втора част (½) от тази
стойност, в
резултат на
която реалната
стойност
![]()
на
числото X се
замества със
стойност,
която се
отличава от
реалната с
абсолютна
грешка
![]()
За
тази грешка
се твърди, че
е по-малка
или равна на
абсолютната
стойност на
непредставената
значеща част
на реалното
число.
Казаното може
да се изрази
формално
така:
![]()
и е
илюстрирано
за двата
възможни
случая чрез
рисунките от
фигура 3.3.1.1.
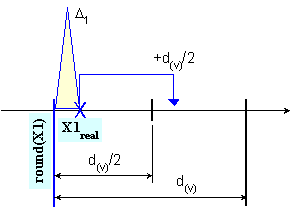
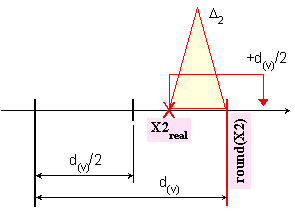
Фиг.
3.3.1.1.
Геометрична
илюстрация
на функция round(X,v)
Схемата
на
заместване
на реалното
число със
закръгленото,
която се
постига с
помощта на
функцията round(X,v), се
определя
като схема за
заместване с най-близко
стоящото
представимо
v-разрядно
число. В
първата
рисунка на
фигура 3.3.1.1 това число
стои отляво
на релното, а
във втората –
отдясно.
Чрез
функцията (3.3.1.14) влизат в
сила
следните
тъждества:
ако a b , то FLOAT(a+c) FLOAT(b+c) ; (3.3.1.16)
и още:
round(-a, v) = -round(a, v) , round[(a.q), v] = q.round(a, v) . (3.3.1.17)
По силата на тези съотношения, при условие, че не настъпва положително или отрицателно препълване в полето на порядъка, са в сила още следните тъждества:
FLOAT(a+b) = round[(a+b), v]
, FLOAT(a-b) = round[(a-b), v]
. (3.3.1.18)
Илюстрацията
на
алгоритмите
за събиране и
изваждане на
числа
представени
във форма с
плаваща
запетая
както без така
и с техниката
на скрит бит
е изложена подробно в книга
[2].
Отново
искаме да
предупредим
читателя, че изложените
тук
съображения
не са достатъчно
изчерпателни.
Темата е
достатъчно
сложна и
многоаспектна,
така че тя ще
бъде
допълвана в
последствите,
когато бъдат
обеснявани
логическите
структури на
устройствата
за обработка
на числа,
представени
във форма с
плаваща
запетая, както
и при други
подходящи
случаи.
Следващият
раздел е:
3.3.2
Операция
умножение ( Operation
multiplication )