3.2.9.3 Схемен
делител. Частно
Hardware divider. Calculation of the Quotient
Операция
деление,
която е
сравнително
рядко
срещана
(вижте
статистическите
оценки в §3.1,
таблица 3.1.1), поради
сложния си
алгоритъм, е
достатъчно бавна,
в сравнение с
останалите
операции
върху цели
числа. По
тази причина
са оправдани
усилията за
нейното ускоряване.
Вече бяха
разгледани
методи за ускоряване
на операция
деление, но
те не гарантираха
това
абсолютно, а
само в
статистически
смисъл. Ето
защо
желанието за
гарантирано
ускорение,
подобно на
операция
умножение
чрез
разработените
за нея
апаратни методи,
остава, и тук
ще
представим
възможностите
за
аналогичен
подход към
операция деление.
Вероятно не е
трудно за
читателя, който
познава
целочислената
аритметика (което
тук
предполагаме
безусловно),
да съобрази,
че най-удобен
в това
отношение се
оказва
етапът на
същинското
деление. Аналогично
на
алгоритъма
за умножение
и тук при
деление, в
този етап, се
изпълняват
множество
последователни
операции от
тип събиране.
Тъй като методите
за деление са
от тип “цифра
по цифра”, за
разлика от
умножение, на
всяка
итерация се
формира една
поредна
цифра за
частното и се
определя
следващата
итерационна
операция. В
следващата
таблица (копие
от раздел 3.2.8) са
припомнени
правилата за
това.
Таблица
3.2.8.1
Определяне
на текущата j-та
цифра в
частното и
следващата
операция
|
Знак на остатъка Rj |
Знак на делителя Wy |
Поредна
цифра в
частното zj |
Следваща
операция Rj+1= |
|
+ |
+ |
1 |
2. Rj - Wy |
|
+ |
- |
0 |
2. Rj + Wy |
|
- |
+ |
0 |
2. Rj + Wy |
|
- |
- |
1 |
2. Rj - Wy |
Ще припомним, че частното се определя след лявата нормализация на делимото X и на делителя Y. Ляво нормализираните операнди бяха означавани с имената WX и WY (или още Wx и Wy).
Ще обърнем внимание на това, че тук по-долу, няма да проектираме цялостната структура на устройството за деление, а само онази част от апаратурата, която ще реализира еднотактното апаратно или още схемно деление. Първият етап от алгоритъма за деление, при който се проверяват логическите условия за дефинираност и изпълнимост на операцията, както и вторият етап, етапа на лявата нормализация на операндите, съдържат действия, които остават не променени. Това означава, че и апаратурата, с която се реализират остава такава, каквато вече е била представена. В представените в предходните раздели устройства за деление, третият етап на същинското деление, се реализира циклически с помощта на един единствен суматор, който е обхванат от няколко обратни връзки, и множество измествания.
Както и при умножение, същността на идеята за апаратно ускоряване при деление се състои в използването на множество суматори, благодарение на което отпада необходимоста от многотактово превъртане на частичните остатъци през един и същи суматор. Така третият етап от алгоритъма за деление (същинско деление) ще бъде реализиран като еднотактна комбинационна схема. Множеството итерации в тази част на алгоритъма ще бъде реализирано апаратно. Това ще бъде постигнато чрез множество суматори и чрез подходящото им опроводяване. За да добие първоначална представа за крайния резултат, който тук по-долу ще получим, читателят може да разгледа комбинационната схема, представена на в книга [3], раздел 4 (продължение 1), фигура 4.12.
Логическата схема ще синтезираме приемайки, че тя ще работи според изискванията на алгоритъма за деление в допълнителен код, по метода без възстановяване на остатъка. При това ще приемем, че читателят перфектно познава този алгоритъм. Същността на този алгоритъм е представена по-горе чрез таблица 3.2.8.1. Според него, след получаване на поредния частичен остатък Rj, в частното следва да се запише поредната цифра zj. Приемайки тази част от таблицата като таблица на истинност, можем да синтезираме логическата функция за стойността на поредната цифра в частното. Нейното уравнение е следното
![]()
Тази
логическа
функция,
както
вероятно читателят
забелязва, е
функцията на
равнозначността,
т.е. ако
знаците на
текущия
частичен
остатък и на
делителя
съвпадат, в
частното се
записва
единица, в
противен
случай нула.
Заедно
със
записването
на поредната
цифра в
частното се
извършва
изместване
наляво на
един бит на
частичния
остатък (има
се предвид
организационната
схема за
деление,
наречена “с
неподвижен
делител”). С
това
изместване
се получава
произведението
2.Rj.
Следващият
частичен
остатък се получава
чрез
изпълнение
на
определената
операция
(събиране или
изваждане)
според най-дясната
колонка в
горната
таблица. Аритметическата
операция в
израза (2. Rj – Wy) или в
израза (2. Rj
+ Wy) изисква
суматор, към
който следва
да се подава
делителят
или неговият
допълнителен
код. Изборът,
както може да
се очаква,
определя
стойността
на функцията
(3.2.9.3.1).
И
така,
завършваме
този етап от
обясненията
с
произтичащата
от тях
логическа
структура,
реализираща
всички
текущи
действия, която
представяме
на фигура 3.2.9.3.1
по-долу.
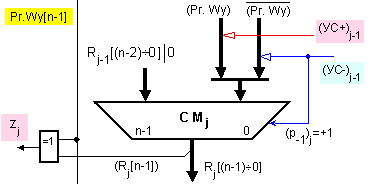
Фиг. 3.2.9.3.1. Логическа
структура на
суматорите в
делителя
(текущо j-то
ниво)
Както
може да се
види, знакът
на делителя Рг.Wy[n-1]
и знакът на
новия
частичен
остатък Rj[n-1]
формират
текущата
цифра в частното
zj .
За да
се получи
текущият
частичен
остатък Rj, на
левия вход на
текущия
суматор СМj
се подава
като първи
операнд
изместеният наляво
на един бит
предходен
частичен остатък
R(j-1).
Изместването
наляво се
разбира от разрядния
указател,
според който
към вход №(n-1) се
подключва
разряд №(n-2), а
към най-младшия
вход №(0) се
подава
конкатенираната
константа
нула (0).
Най-младшият
вход получава
цифра нула (0)
тъй като при
изместването
той остава
свободен. С
други думи,
изместената
наляво сума
се конкатенира
отдясно с
цифра нула и
така се подава
на суматора,
което в
рисунката е
записано така:
R(j-1)[(n-2)…0]│0.
По
десния вход
на суматора,
чрез
двувходовия
мултиплексор,
се подава за
събиране или за
изваждане
нормализирания
делител Wy. Той се
явява съдържание
на регистър Рг.Wy.
Управлението
на десния
вход на
суматора е многократно
обяснявано в
тази книга.
То реализира
операциите
събиране и
изваждане в
допълнителен
код чрез
управляващите
сигнали (УС+) и
(УС-).
Логическите
стойности на
тези сигнали
са кодирани
според
следната
логическа
функция:
![]()
Тъй
като
частното е
число със
знак и се
получава
автоматично
в
допълнителен
код, неговата
цифрова част
има
дължината (n-1)[b]
(тук с n е
означена
дължината на
разрядната
мрежа). От тук
следва, че
схемният
делител
трябва да има
(n-1)
на брой нива,
за да изчисли
(n-1)
на брой
цифри. Ще
припомним, че
преди етапа на
същинското
деление, след
сравняване
на знаците на
операндите,
се определя
знакът на
частното,
чиято
стойност
определя
началното
съдържание
на регистъра
на частното,
в това число и
стойността
на знаковия
бит с номер [n-1].
Така вдясно
от
предварително
определения
знак ще се
подредят (n-1) на
брой цифри на
частното.
Означената
като обща
разрядност
затруднява
изчертаването
на
принципната
логическа
схема на
делителя, ето
защо ние, без
загуба на
общност, ще я
ограничим и
конкретизираме
до n=8[b],
аналогично
както при
схемния умножител,
който беше
посочен
по-горе като пример.
Последното,
което трябва
да бъде
изяснено, е
свързано с
това, че при
този
алгоритъм,
частното не
винаги се
получава
точно, което
се дължи на
несиметричността
на
допълнителния
код.
Правилата за
корекция на
частното са
припомнени
тук от следващата
таблица,
която беше
създадена в раздел
3.2.8.
Таблица
3.2.8.2
Определяне
на корекцията
|
Знак на
делимото X |
Знак на
делителя Y |
Стойност
на
корекцията |
|
+ |
+ |
няма
корекция |
|
+ |
- |
+1 |
|
- |
+ |
+1, ако
Rk-l+1 ¹ 0 |
|
- |
- |
+1, ако
Rk-l+1 = 0 |
В тази
таблица с Rk-l+1 е
означен
последният
частичен
остатък. Ще припомним,
че в етапа на
лявата
нормализация
на
операндите
се определя
числото N=k-l+1 (вижте
уравнение (3.2.6.5)),
показващо
броя на
неизвестните
цифри на частното.
С k и l са
означени
съответно
реда на
полинома на делимото
и на
делителя.
Както
се вижда от
таблицата,
когато частното
не е вярно, то
се коригира,
като към младшия
му бит се
добавя
единица. Това
разбира се е
свързано с
необходимостта
от разпознаване
на
съответните
ситуации,
както определя
таблицата.
Разпознаването
или още дешифрирането
на
необходимостта
от корекция осъществява
логическа
функция,
която зависи
от знаците на
операндите, а
в последните два
случая и от
това, дали
делението е
точно или не.
Ако на
таблица 3.2.8.2 се
гледа като на
таблица на
истинност,
може да се
съобрази, че
логическата
функция,
изразяваща необходимостта
от корекция
на частното,
е дизюнкция
от три
логически
терма
![]()
където
cor (correction). Първият
терм
изразява
условието за
корекция от
втория ред на
таблицата
![]()
Вторият
и третият
терм (cor2 и cor3) са
функции за
корекция,
отнасящи се
за третия и
съответно за
четвъртия
случай в
таблицата за
корекции. От
една страна
тези функции
също зависят
от знаците на
операндите, както
и от
стойността
на последния
частичен
остатък, т.е.
от това дали
делението е
точно или не.
Така за тези
логически
функции можем
да запишем
следните
изрази:
![]()
![]()
В
горните
изрази с EQ(R) е
означена
логическата
стойност на
функция,
която
дешифрира
нулев
частичен
остатък в
произволна
итерация
(произволно
ниво) по
време на делението.
Тъй като този
факт трябва
да се дешифрира
на всеки
такт, тази
функция
трябва да има
следния
събирателен
вид:
![]()
Искаме
да обърнем
внимание на
това, че според
разбирането
на
традиционния
алгоритъм за
деление,
последният
частичен
остатък има
изключително
сложно определение
за това че е последен.
Например, той
е последен,
ако са
получени всички
неизвестни
цифри на
частното, т.е.
ако са
получени
всички N на брой
цифри. Но има
случаи на точно
преждевременно
деление, при
това след
различен
брой тактове,
преди
изчерпване
на
контролното
число N. В
смисъла на
преследваната
тук задача,
т.е. в смисъла
на
апаратното
реализиране
на процеса на
деление, определянето
на остатъка
като
последен е крайно
неудобно,
тъй като той
може да се
получи в
произволно
ниво на
логическата
схема на
делителя. Ето
защо
изказването,
че делението
е точно, ако
частното
няма дробна
част,
представлява
изключително
удобна интерпретация
за това дали
е необходима
или не корекция
в последните
два случая на
таблицата.
За да
можем
по-лесно да
обясним
синтеза на логическите
функции cor2 и cor3,
както и
апаратните
решения,
свързани с
тях, ще
представим
няколко
числени
примери,
илюстриращи
различните
случаи, в
които се
налага
корекция на
полученото
частно.
ПРИМЕР 1. С
този пример
ще
илюстрираме четвъртия
случай
(деление на
две
отрицателни
числа), при
който
корекция се
налага,
когато делението
е точно.
Да
се изпълни
операция
деление Z=X/Y на
числата X=-84 и Y=-7,
които са
представени
в разрядна
мрежа с
дължина n=8[b] в
допълнителен
код. Z=12.
Дм =
![]() = 1 0101100 ; Дт
=
= 1 0101100 ; Дт
= ![]() = 1 1111001.
= 1 1111001.
Лява
нормализация
на
операндите:
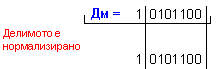

N = 4 - 0
+ 1 = 5 (5
неизвестни
цифри на
частното).
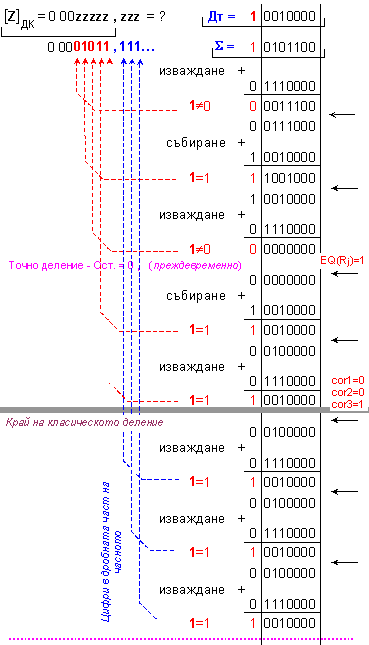
![]() = 0 0001011 - този
резултат не е
верен!
= 0 0001011 - този
резултат не е
верен!
Според
четвъртия
случай на
деление
(таблица 2), при
точно
деление е
необходима
корекция +1.
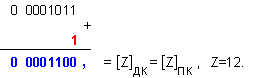
Забележка:
Извършваме
корекция
върху реалния
резултат
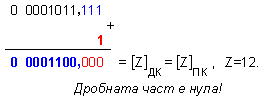
ПРИМЕР 2. С
този пример
ще
илюстрираме третия
случай
(деление на
отрицателно
с положително
число), при
който
корекция се
налага,
когато
делението е
неточно.
Да
се изпълни
операция
деление Z=X/Y на
числата X=-84 и Y=7,
които са
представени
в разрядна
мрежа с дължина
n=8[b] в
допълнителен
код. Z=-12.
Дм =
![]() = 1 0101100 ; Дт
=
= 1 0101100 ; Дт
= ![]() = 0 0000111.
= 0 0000111.
Лява
нормализация
на
операндите:
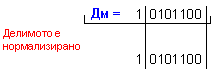

N = 4 - 0
+ 1 = 5 (5
неизвестни
цифри на
частното).
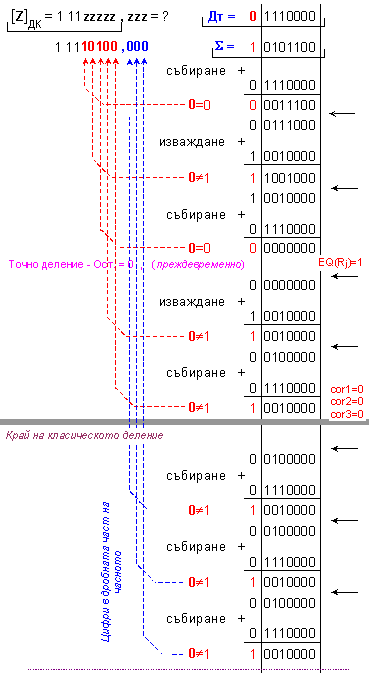
![]() = 1 1110100 - този
резултат е
верен!
Z=-12.
= 1 1110100 - този
резултат е
верен!
Z=-12.
Според
третия
случай на
деление
(таблица 2), при
точно
деление не е
необходима
корекция!
Обърнете
внимание – дробната
част е нула!
ПРИМЕР 3. С
този пример
ще
илюстрираме втория
случай
(деление на
положително
с отрицателно
число), при
който
корекция се
налага
винаги.
Да
се изпълни
операция
деление Z=X/Y на
числата X=84 и Y=-7,
които са
представени
в разрядна
мрежа с дължина
n=8[b] в
допълнителен
код. Z=-12.
Дм =
![]() = 0 1010100 ; Дт
=
= 0 1010100 ; Дт
= ![]() = 1 1111001.
= 1 1111001.
Лява
нормализация
на
операндите:
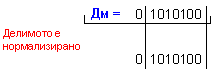

N = 4 - 0
+ 1 = 5 (5
неизвестни
цифри на
частното).
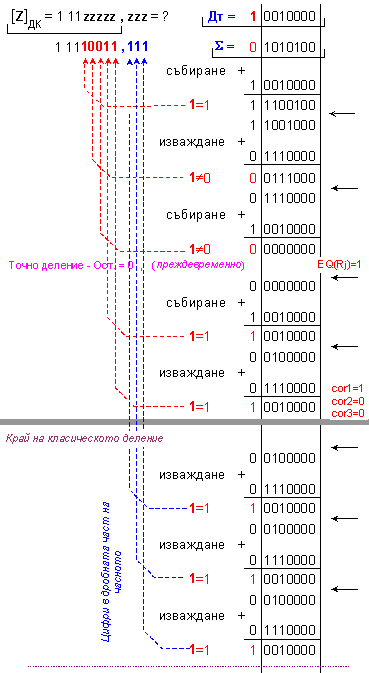
![]() = 1 1110011 - този
резултат не е
верен!
= 1 1110011 - този
резултат не е
верен!
Според
втория
случай на
деление
(таблица 2), винаги
е необходима
корекция.
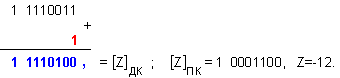
Забележка:
Извършваме
корекция
върху реалния
резултат
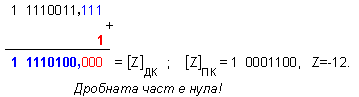
ПРИМЕР 4. С
този пример
ще
илюстрираме четвъртия
случай
(деление на
две
отрицателни
числа), при
който
корекция се
налага,
когато делението
е точно. В
този пример
делението не
е точно.
Да
се изпълни
операция
деление Z=X/Y на
числата X=-100 и Y=-7,
които са
представени
в разрядна
мрежа с
дължина n=8[b] в
допълнителен
код. Z=14.
Дм =
![]() = 1 0011100 ; Дт
=
= 1 0011100 ; Дт
= ![]() = 1 1111001.
= 1 1111001.
Лява
нормализация
на
операндите:
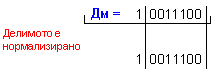

N = 4 - 0
+ 1 = 5 (5
неизвестни
цифри на
частното).
Същинско
деление:
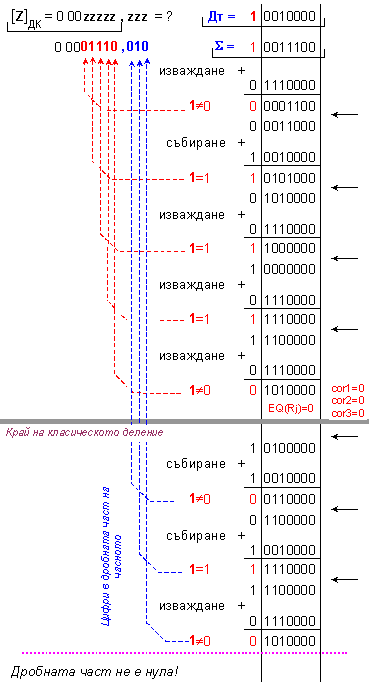
![]() = 0 0001110 - този
резултат е
верен!
Z=14.
= 0 0001110 - този
резултат е
верен!
Z=14.
Според четвъртия случай на деление (таблица 2), при неточно деление не е необходима корекция.
Представените
примери са
интересни
още и с това,
че процеса на
деление не е
стопиран нито
при
преждевременното
точно
деление, нито
след
изчисляване
на всички
неизвестни
цифри в
частното.
Краят на
класическото
деление в
примерите е
маркиран с
по-дебела
сива линия,
след която,
според
логиката на
алгоритъма,
са изчислени
още няколко
цифри, които
както може да
се види,
принадлежат
на дробната
част на частното.
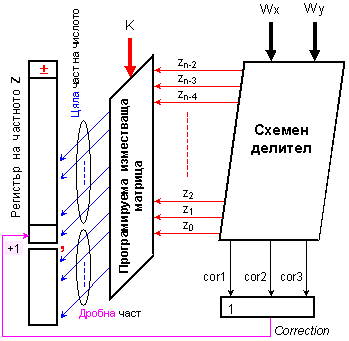
Фиг. 3.2.9.3.2.
Структура
на
апаратурата
за етапа на
същинското
деление
Както
се вижда, на
схемния
делител се
подават двата
ляво
нормализирани
операнда,
чиито знаци
определят
началното
съдържание
на регистъра
на частното Рг.Z.
От делителя
излизат (n-1) на
брой цифри на
частното (zn-2, zn-3,
… z1, z0), както и
трите терма
на функцията
за корекция (cor1,
cor2, cor3). Частното е
подадено на дясно
изместваща
програмируема
матрица. Синтезът
на различни
програмируеми
изместващи
матрици вече
беше
представен в
раздел §3.5 Логически
операции,
сравнения,
измествания, по
тази причина
тук върху
тази
логическа
схема няма да
се спираме.
Както се
вижда от
рисунката,
тази схема се
програмира
за
изместване
от
параметъра K.
Броят на
изместванията
се определя
така:
![]()
Стойността
на
параметъра K
може да бъде
изчислен още
на етапа на
лявата
нормализация,
когато се
изчислява и
стойността
на N (брой на
неизвестните
цифри в
частното).
След това,
тази
стойност трябва
да се
съхранява в
отделен
регистър до края
на
операцията
(РгК).
Що се
отнася до
самата
корекция, то
горната схема
илюстрира
как
изместеният
и
позициониран
спрямо правилното
място на
запетаята
резултат, се
събира със
стойността
на функцията
COR (0 или 1),
подавана в
младшия
разряд №0.
Дробната част
на частното в
случая
оставяме
само за илюстрация.
Тя без
корекцията е
невярна и
следва да се
изхвърли. Ако
все пак
искаме да я
съхраним, то
корекцията (+1)
трябва да се
подава не в
младшия бит
на цялата
част (b0), а в
най-младшия
фиксиран бит
на реалното частно.
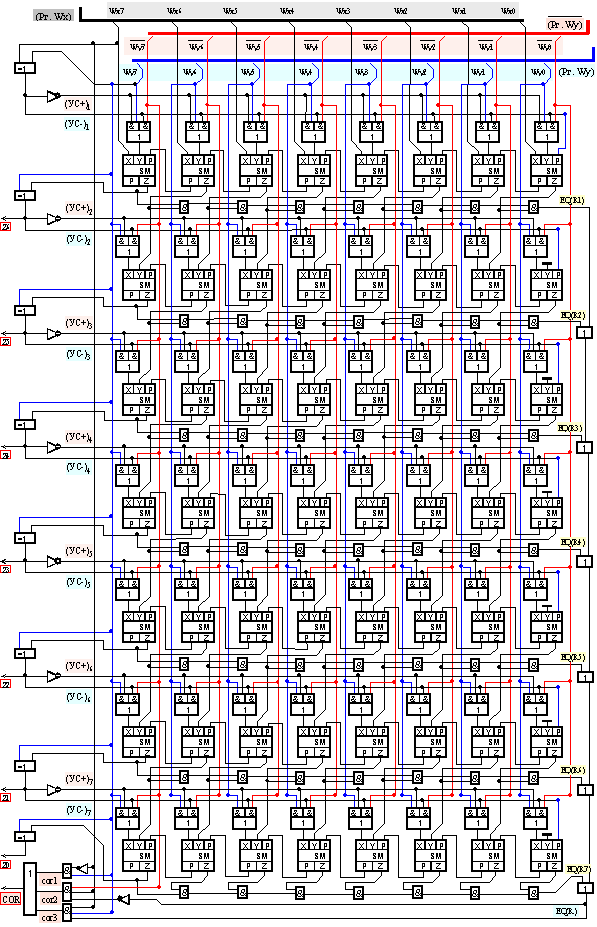
Фиг. 3.2.9.3.3.
Принципна
логическа
схема на схемен
делител 8/8
Както
беше
отбелязано
по време на
анализа, не е
възможно
апаратното
решение на
същинското
деление да
постигне
онази
динамика,
която е присъща
на
алгоритъма.
Има се
предвид
променливата
дължина на
числото,
изразяваща
се чрез
параметъра N.
Дължината на
частното се
адаптира в
схемата чрез
параметъра K,
който инициализира
програмируемата
изместваща матрица.
Функционирането
на
апаратното
решение
обаче
благоприятства
използването
му в случай
на деление на
числа с плаваща
запетая.
Както е
известно,
мантисите на
операндите са
винаги ляво
нормализирани
числа, от където
следва, че
частното се
получава
винаги с една
и съща
дължина. С
други думи,
при деление на
числа с ляво
фиксирана
запетая,
схемният
делител не
зависи в своя
синтез от
параметъра N и в
неговата
структура не
е необходима
програмируемата
изместваща
матрица.
С
това считаме
изложението
на темата за
завършено.
Има разбира
се още
няколко
подробности,
които си
спестяваме,
което правим
винаги,
когато
искаме да
поощрим
любознателният
читател.
Например за
случаите, в
които се
налага
нормализация
на
полученото
частно след
деление на
числа с ляво
фиксирана
запетая или
пък случая с
препълване
при деление
на цели
числа. За
отразяване
на тези тънкости
в
синтезираната
схема е
необходимо само
добро
познаване на
алгоритъма.
Следващият
раздел е:
3.2.9.4 Схемен
делител. Остатък ( Hardware divider. Calculation of
the Remainder )