3.2.6
Операция
деление
Division
Операция
деление Z=X/Y е
производна
от операция
изваждане.
Нейните
операнди се
наричат делимо (Дм) - X и делител
(Дт) - Y, а
резултатът Z се
нарича частно.
Това е
главният
резултат. По
определение (в
контекста на
числата с
дясно
фиксирана
запетая)
частното се
търси като
число, което
показва колко
пъти
делителят се
съдържа в
делимото.
От това
определение
следва, че
операцията е изпълнима,
ако е
изпълнено
съотношението:
![]()
Ако
(3.2.6.1) не е
изпълнено, то
операцията е неизпълнима,
а резултатът
е нула, т.е.
делителят не
се съдържа в
делимото или
се съдържа нула
пъти (Z=0). В
частност,
когато
делителят е
нула, операцията
е не само
неизпълнима
но и недефинирана,
тъй като по
определение,
резултатът
от деление на
нула се
приема за
абстракцията
безкрайност (±¥), която е
непредставима
в разрядната
мрежа и във
формата с
фиксирана
запетая се
сигнализира
чрез
признака за
препълване: V=1.
От
определението
на
операцията
следва и най-елементарният
алгоритъм за
нейното
изпълнение, а
именно, че
частното Z се
намира чрез преброяване
на
последователните
успешни
изваждания
на делителя
от делимото,
докато се
получи
разлика,
чиито модул е
по-малък от
модула на
делителя.
Тази
последна
разлика се
нарича остатък, а
всички предидущи
- частични
остатъци.
От
изказаното
определение
се вижда
пряката
връзка с
операция
изваждане. По
своята структура
този
алгоритъм е
циклически - от
вида с
предварително
неизвестен
брой повторения.
Според изказания алгоритъм е в сила следната обратна връзка между операндите и резултатите:
![]()
където с Rx е
означен остатъкът
от делението,
т.е.
останалото
от делимото X цяло
число, което
не съдържа
вече
делителя, тъй
като
![]()
Остатъкът
е цяло число.
Когато
числата са
със знак
остатъкът
носи знака на
делимото,
което вече
беше
пояснено в
глава 1. Тук обаче
трябва да
допълним
особеностите
на операция
деление,
които я
определят
като една от
най-сложните.
В много
случаи
математическите
методи
изискват
като
резултат именно
остатакът от
целочисленото
деление. Ето
защо
читателят
трябва да
знае, че
компютърната
реализация
на операция
деление, за разлика
от всички
останали,
определя 2
резултата – частно и
остатък.
Ако
Rx=0,
делението е точно,
т.е.
полученото
частно е цяло
число. Ако Rx≠0,
то делението
е неточно,
или още с
остатък.
Според (3.2.6.2)
частното Z е
цяло число,
което в смисъла
на
определението
приемаме за вярно.
Получаването
само на този
резултат се
нарича целочислено
деление. Той
е интересен с
това, че е
представен в
същата форма,
в която са
представени
и двата
операнда. С
други думи, в
общия случай частното
е реално
число, т.е.
число с цяла
и дробна
част.
В заключение следва да обърнем внимание на читателя, че операция деление е съществено различна по своите характеристики от останалите целочислени операции. Тя може да бъде неопределена, неизпълнима, точна или неточна и в общия случай частното е реално число. Последното налага разглеждането на резултат от същия тип (същата форма) спрямо операндите, случай който определихме като целочислено деление.
Изказаният по-горе алгоритъм по определение може да се реализира най-лесно в логическата структура на устройство за изваждане с добавен към нея сумиращ брояч за формиране модула на частното. Условието за край на делението е получаване на нулев частичен остатък (при точно деление) или частичен остатък с отрицателен знак (при неточно деление). Това условие може да бъде разпознато по признаците на резултата, фиксиран на изхода на суматора. Продължителността на този изчислителен процес обаче ще се изменя в твърде широки граници, тъй като тя зависи от силата на неравенство (3.2.6.1), което определя броя на операциите изваждане. Ето защо алгоритъмът за деление по определение практически не се реализира апаратно, особено в условията на двоична бройна система.
Както
за операция
умножение,
така и за
операция
деление, се
търсят
алгоритми за
реализация,
които
гарантират
предварително
нейното
времетраене.
За техния
синтез следва
да бъдат
взети под
внимание
всички характеристики
на числата.
Естествено
при това на
първо място трябва
да бъде
отчетен
фактът, че
числата са представени
в позиционна
бройна
система, а на
второ място
следва да се
отчете, че те
са в двоична
бройна
система. В
този случай
делимото X е
полином
примерно от k-ти ред
![]()
делителят
Y е
също полином,
но от l-ти ред
![]()
при
което според
(3.2.6.1) излиза, че (k ³ l).
Тогава
частното Z е
полином от
ред (k-l),
т.е.
![]()
което от своя страна означава, че частното има (k-l+1) на брой неизвестни цифри в цялата си част.
Тъй
като от
гледна точка
на
алгоритъма
за деление,
числата k и l са
без значение
или по-точно
са
неизвестни, то
те не могат
да се
използват за
непосредственото
определяне
на реда на
полинома на частното.
Като се има
предвид
обаче, че
модулите и на
двата операнда
X и Y са
записани в
поле с
константна
дължина (n
разряда –
имаме
предвид
разрядната
мрежа с дясно
фиксирана
запетая,
представена
на фигура 1.1.6.1.3),
то чрез една
лява
нормализация
на операндите
тази величина
може да бъде
определена.
Лявата
нормализация
практически
представлява
изместване
на числата в
разрядната
мрежа наляво,
докато се
превърнат в
полином от (n-2)-ри
ред (вижте
фигура 1.1.6.1.3, т.е.
превръщат се
в числа,
които
удовлетворяват
неравенството
![]()
Тогава
неизвестната
разлика (k-l) може
да бъде
определена
чрез
известните измествания
на
операндите,
направени
при тяхната
лява
нормализация
по следния
начин: ако
броят на
изместванията
на делимото е
бил Lx,
а на
делителят Ly, то
![]()
Ще
илюстрираме
това със
следващата
рисунка
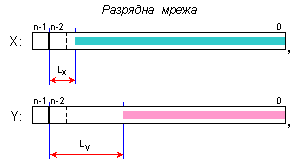
Чисто
геометрично
може да се
забележи, че
разликата
между
дължините на
операндите, е
равна на
разликата
между
дължините на
старшите
“празни”
участъци в
разрядната
мрежа.
Ето
защо това
равенство
може да се
докаже по
следния
начин:
изместването
наляво на делимото
и делителя
представлява
привеждане
на реда на
техните
полиноми към
едно и също
число - (n-2), т.е.
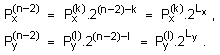
Следователно
(k-l)
трябва да е
разликата (Ly - Lx):
![]()
с което
се доказва,
че с помощта
на числата Lx и Ly,
определяни в
процеса на
лявата
нормализация
на
операндите,
могат да
бъдат
изчислени
редът на
полинома на
частното и
броят на неговите
неизвестни
цифри:
![]()
Делението на два полинома трябва да представлява процес, в който се определя:
·
С
нарастваща
точност
частното;
·
Или
се определя
последователността
от цифри на
частното.
Това по същество представляват две различни направления в разработване на методите за машинна аритметика и в частност при разработване на методите за деление.
Tук
на първо
място ще
бъдат
разгледани
методи и
алгоритми,
представители
предимно на второто
направление,
при които
частното се
получава цифра
по цифра. На
практика
това са алгоритмите,
намерили
най-широко
приложение.
По-подробно с
методи,
представители
на първото
направление,
читателят
може да се
запознае в книга
[2].
И
така,
делението на
два полинома
се дефинира
математически
еднозначно
като полином
по следния
начин:
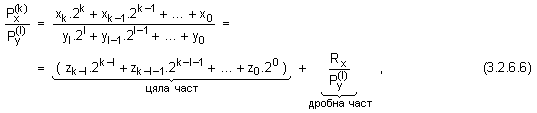
където
последователността
от двоични цифри { zk-l
zk-l-1
… z1
z0 } (коефициенти
на полинома
на цялата
част на частното)
представляват
неизвестните
цифри на
частното.
Ако се изравни редът на полинома на делителя до този на делимото ще получим следното:
![]()
Ясно
се вижда, че в
цялата част
на новото частно
остава само
една значеща
цифра - zk-l. Веднага
следва да
обърнем
внимание на
факта, че
това е
най-старшата
цифра на
търсеното
частно.
Смисълът на
тази цифра
произтича от
определението
- тя
показва
колко пъти
нормализираният
(спрямо
делимото)
делител се
съдържа в
делимото. Определянето
на тази цифра
може да стане
само по
определението
за операция
деление, т.е.
чрез
последователно
изваждане на
нормализирания
делител от
делимото.
Тези
изваждания
трябва да се
извършват докато
не се получи
отрицателна
разлика, т.е. докато са
възможни по
определение.
В общия
случай броят
на
изважданията,
при които се
получава
положителна
разлика, не
може да бъде
повече от
числото (q-1), където q
е основата на
бройната
система, при
положение, че
полиномите в
разликата са
от един и същи
ред. Това
означава, че в
двоична
бройна
система
нормализираният
делител се
съдържа не
повече от
един път в
делимото.
Тогава за
установяване
на този факт
е необходимо
и достатъчно
да се извърши
само
едно
изваждане.
От
горното
заключение
следва
твърде простото
правило за
определяне
на цифрата zk-l в
случай на
двоична
бройна
система:
![]()
В
горното
определение,
с R1 е
означена
първата
разлика
между делимото
и
нормализирания
делител.
Може
да се твърди,
че след
определяне
на цифрата zk-l, редът на
двоичния
полином на
разликата R1 е
понижен поне
с единица и
той е от ред (k-1).
За
определяне
на
следващата
цифра zk-l-1 в частното е
необходимо
да се
възстанови
нормализираният
вид на
разликата R1 спрямо
нормализирания
делител, ако
искаме да
приложим
определението
(3.2.6.7).
Изравняването
на редовете
на
полиномите
на получената
разлика и на
делителят
може да се
постигне по
два начина:
·
Изравняване
реда на
полинома на
разликата до
този на
делителя,
което може да
се постигне
чрез
изместване
наляво на разликата
спрямо
делителя на
един разряд;
·
Или
изравняване
реда на
полинома на
делителя до
този на
разликата,
което може да
се постигне
чрез
изместване
надясно на
делителя
спрямо
разликата на
едни разряд.
След
възстановяване
на
съвместния
нормализиран
вид на двата
полинома - R1
и Py
(според
първия от
посочените
току що начини),
същите се
подлагат
отново на
деление, което
се реализира
отново по
същия начин,
т.е. по
определение.
Резултатът в
смисъла на
целочисленото
деление
![]()
е цифрата
zk-l-1 и новата
разлика R2.
Процедирайки
по този начин
– с
изравняване на
реда на
двоичните
полиноми и
делейки ги по
определение
могат да
бъдат
определени последователно
всички
останали
младши цифри
на частното.
Този процес
на
последователно
нормализиране
и изваждане
по същество
изразява
най-общо
алгоритъма
за деление. В
него прозира
основната му
характеристика
-
продължителността
му вече не
зависи от модулите
на
операндите, нещо
повече - може да
се каже, че
този
алгоритъм
има толкова
стъпки,
колкото са
неизвестните
цифри на
частното. И
тъй като те
не могат да
бъдат повече
от (n-1), то
максималният
брой тактове
няма да надхвърля
това число.
Очевидно
описаният
процес
определя частното
последователно,
цифра по
цифра,
започвайки
от старшата,
и
следователно
той може да
се оприличи
на процес,
при който с всеки
нов такт
частното се
определя с
повишаваща
се на порядък
точност. В
този смисъл процесът
на деление,
описан
по-горе, може
да се изрази въз
основа на
израза (3.2.6.2) чрез една
рекурентна
зависимост,
по която се
получават
междинните
разлики
![]()
наричани
още частични
остатъци:
![]()
където
![]()
e
първоначално
нормализираният
делител.
В
рекурентната
формула (3.2.6.9)
произведението
(Rm.q) изразява
предварителната
нормализация
на m-тата
разлика
спрямо
делителя.
След получаване
на следващия
частичен
остатък Rm+1, чрез
правилото (3.2.6.8)
се определя
следващата цифра
в частното - zm+1, след което
отново може
да се приложи
рекурентната
формула за
получаване
на частичния
остатък Rm+2.
Тук
обаче трябва
да се обърне
внимание на факта,
че в
рекурентната
формула (3.2.6.9) по
същество е
изразена
операцията аритметическо
изваждане,
която
реализира
операция
деление само
когато е
изпълнено
съотношението
(3.2.6.1) за всеки
частичен
остатък. В
общия случай
аритметическите
изваждания
могат да
бъдат
няколко, но
не повече от (q-1), т.е. те
са в
зависимост
от основата
на бройната
система.
Условието да
бъдат
прекратени
тези
аритметически
изваждания,
представляващи
процеса на
определяне
на поредната
(m-та) q-ична
цифра на
частното, е
получаването
на
отрицателна
разлика. С
други думи, в
общия случай,
процесът на
получаване
на поредната
цифра в
частното завършва
винаги с
отрицателен
(или нулев)
частичен
остатък. В
двоична
бройна
система
обаче, както
вече беше
казано,
предварително
е известно,
че
изваждането
е само едно и
то е достатъчно
за да може
правилото (3.2.6.8)
да определи
поредната
цифра в
частното. Ако
полученият
частичен
остатък е отрицателен,
то
рекурентната
формула (3.2.6.9) не
може да се
приложи
веднага,
защото в нея
умаляемото
ще бъде
отрицателно
число, което
при операция
аритметическо
изваждане ще
доведе
практически
до изпълнение
на операция
аритметическо
събиране,
която не
съответствува
на
изпълнение
на операция
деление по
определение.
Нещо повече,
получената
отрицателна
разлика не
представлява
поредния частичен
остатък.
Нейното
получаване в
общия случай
е необходимо
само за да
бъде разпознат
моментът, в
който
поредната
цифра на
частно е вече
определена.
Истинският
частичен
остатък е
онова
умаляемо, от
което се е
получила отрицателната
разлика.
Следователно
за да бъде
продължен
процесът на
деление, трябва
преди да се
приложи
рекурентната
формула, да
се
възстанови
частичният
остатък. Той
може да се
възстанови
по обратен
начин, като към
получената
отрицателна
разлика се
прибави
умалителят.
Току
що
изказаният
алгоритъм за
деление се
нарича алгоритъм
за деление с
възстановяване
на остатъка
и се представя
със следната
изчислителна
схема:
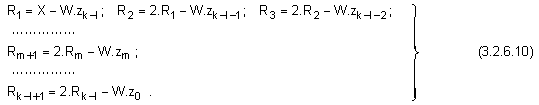
Като
се заместят
последователно
изразите за
частичните
остатъци,
последният
остатък може
да се запише
така:
![]()
или още:
![]()
Искаме да заострим вниманието на читателя върху горния резултат. Нека да обърнем внимание на дясната част на равенството:
1. Ако делението е завършило и Z е полученото целочислено частно, то е в сила отношението
![]()
От това отношение следва изводът, че разликата (X-Z.Y) ще носи знака на делимото X.
2.
Записаната
разлика
представлява
![]()
А сега да обърнем внимание на лявата част на равенството (3.2.6.10.а). Лесно се забелязва, че след заместване може да запишем следното
![]()
Горното равенство е забележително с това, че то изразява как може да се получи вторият резултат от операция деление, а именно остатъкът Rx от делението. Окончателният извод е, че остатъкът Rx се съдържа в последния частичен остатък Rk-l+1, който следва да се измести на (k-l) бита надясно, за да се представи като цяло число. Това число е със знак и ще бъде получено автоматично в допълнителен код.
Така
описаната
част от
алгоритъма
за деление
относно
остатъка е
илюстрирана
с множество
примери,
които са
обособени в
отделен
раздел на книга [2].
Връщайки се на (3.2.6.10а) можем да запишем окончателният резултат, т.е. частното, така:
![]()
където,
припомняме, с
W е
означен ляво
нормализираният
делител.
Процесът на деление по определение може да бъде реализиран и без процедурата за възстановяване на остатъка, която неявно се съдържа в по-горе представената схема (3.2.6.10). За целта при получаване на отрицателна разлика е необходимо операцията изваждане да се реализира не като аритметическа, а като алгебрическа. В условията на двоична бройна система, когато се получи положителен частичен остатък, за определяне на следващия остатък може да се приложи формулата (3.2.6.9). А когато се получи отрицателен остатък, може да се приложи следната формула:
![]()
т.е
операция
събиране в
допълнителен
код.
Валидността на тази формула може да се докаже чрез процедурата за възстановяване на остатъка, която се изразява така:
![]()
Както
се вижда,
преобразуваният
израз съвпада
с израза в (3.2.6.12), който
може да се
обобщи за
произволна
основа на
бройната
система q
така:
![]()
Този
алгоритъм, в
който се
работи с
двете рекурентни
формули (3.2.6.9) и (3.2.6.13),
се нарича алгоритъм
за деление без
възстановяване
на остатъка.
Според този
алгоритъм,
знакът на
текущия
остатък
определя
както
текущата
цифра в
частното,
така и избора
на
рекурентна
формула:
![]()
Алгоритъмът
с
възстановяване
на остатъка
не намира
практическо
приложение
главно по
причина на
допълнителните
операции събиране
възстановяващи
частичните
остатъци,
които
толкова
елегантно
отпадат в
алгоритъма
без
възстановяване.
Окончателно може да се обобщи, че операция деление се изпълнява в следните няколко етапа:
1.
Проверка на
условията за
дефинираност
и изпълнимост
(3.2.6.1) ;
2.
Нормализиране
на делителя и
делимото относно
левия край на
разрядната
мрежа, при което
се определя
броят на
неизвестните
цифри на
частното ;
3.
Същинско
деление. Има
се предвид
както получаването
на частното,
така и на
остатъка.
Необходимо
е да се
уточни, че до
момента
ставаше дума
за деление на
числа по
модул. В
случай, че
числата са
представени
в прав код,
модулът на
частното се
получава по
описания
начин, а в последствие
му се
приписва
знакът, който
се определя
чрез
функцията за
логическа неравнозначност
(3.2.2.2).
В
случай, че
операндите
са с ляво
фиксирана
запетая, те
могат да се
приемат за
нормализирани,
тъй като
представляват
полиноми от
един и същи
ред -
нулев. Броят
на
неизвестните
цифри на частното
в този случай
е n.
От
казаното до момента
става ясно,
че за
реализиране
на операция
деление е
необходимо
устройство, в
което да се
изпълняват
операции
събиране, изваждане
и изместване.
Преди да
изложим обаче
синтеза на
това
устройство е
необходимо
да
анализираме
възможностите
за организиране
на неговата
логическа
структура.
Така като и
при операция
умножение и
тук разновидностите
се определят
в зависимост
от това, какво
ще бъде
изместването.
Възможни са
две схеми за
организация:
- с
неподвижен
делител и
изместващ се
наляво
частичен
остатък;
- с
неподвижен
частичен
остатък и
изместващ се
надясно
делител.
Организационната схемата с неподвижен делител е представена на фигура 3.2.6.1.
В нея се съдържа един суматор, в който първоначално се поставя делимото, един регистър за делителя и един изместващ регистър за частното. Всички логически възли в тази схема са с единична дължина, а изместванията са в една и съща посока.
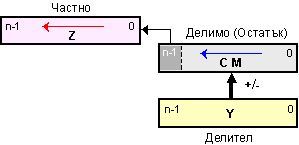
Фиг.
3.2.6.1.
Организационна
схема за
деление с неподвижен
делител
Схемата с неподвижен остатък има в състава си същите възли, но с друга размерност - така например за да е възможно изместване на толкова разряди, колкото са разрядите на неизвестното частно, регистърът на делителя трябва да бъде с двойна дължина, както е показано на фигура 3.2.6.2. Двойната дължина на суматора се налага от изместващия се делител.
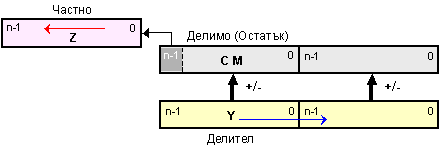
Фиг. 3.2.6.2. Организационна
схема за
деление с неподвижен
частичен
остатък
Очевидно е предимството на схемата с неподвижен делител, която ще бъде избрана като основа за синтез на устройство за деление. Реализацията на тази схема може да се основава както на комбинационен, така и на натрупващ суматор. Тук ще се ограничим само с една от възможностите.
Базовата логическа структура на устройството за деление, показана на фигура 3.2.6.3, е основана на комбинационен суматор.
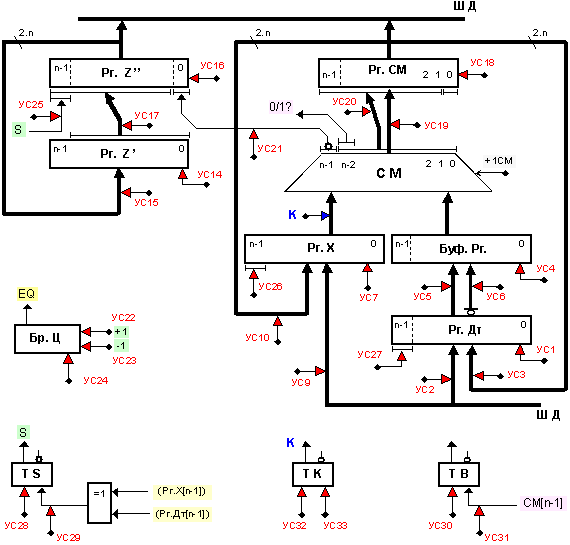
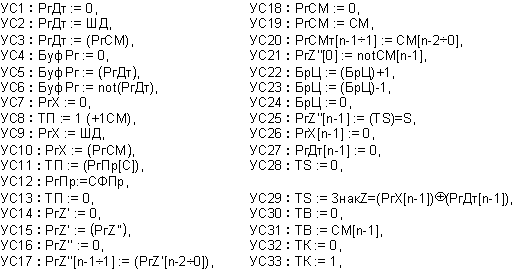
Фиг. 3.2.6.3. Базова
логическа
структура на
устройство
за деление на
числа
представени
в прав код, без
възстановяване, по
схемата с
неподвижен
делител
Както
може да се
види
логическата
структура
съдържа
устройство
за събиране,
което е в
съответствие
с показаното
на фигура 3.2.1.1;
един
изместващ
наляво
регистър за
частното РгZ;
брояч на
циклите БрЦ,
формиращ
условието за
край на
циклическия
алгоритъм EQ=? и
три тригера –
за знака на
частното TS,
за знака на
частичния
остатък TB и
за
управление
на ключа К – TK. В
тази
структура
операндите
се приемат така:
делимото в РгХ,
а делителят в
РгДт.
С
помощта на
косата
връзка от
суматора СМ към РгСМ и
преките
обратни
връзки от РгСМ към РгX и РгДт,
съдържанието
на
последните
може да бъде
измествано
наляво през
суматора.
Това изместване
се изпълнява
при лявата
нормализация
на
операндите.
Изместващият
регистър РгZ ще приема
цифрите на
частното,
които както
вече
обяснихме се
определят
последователно
една по една,
започвайки
от старшите
напред. Ето
защо
началната
стойност на
този
регистър при
работа в прав
код е нула. Броячът
БрЦ е
предназначен
да определи
броя на
неизвестните
цифри на
частното при
лявата нормализация
на
операндите, а
в последствие
чрез
дешифриране
на
вътрешното
състояние (БрЦ)=0 да
формира
условието за
край на
цикъла – според
схемата (3.2.6.10).
Тригерът TS запомня
знака на
частното
веднага след
зареждане на
операндите, а
тригерът TB запомня на
всеки
отделен такт
знака на
получената
разлика (на
частичния
остатък), тъй
като той след
последващата
лява
нормализация
се губи. По
късно (след
лявото
изместване
на разликата)
този знак се
използва за
да се определи
следващата
операция
според алгоритъма
без
възстановяване
на остатъка.
В логическата структура от фигура 3.2.6.3 умишлено не са представени възлите и връзките за формиране на признаците на резултата, но практически те съществуват и съответстват на тези, показани на фигура 3.2.1.1. Обратните връзки:
от РгZ’’ към
РгZ’, управлявана
от УС15;
от РгСМ
към РгX,
управлявана
от УС10;
от
РгСМ
към РгДт
управлявана
от УС3,
в
логическата
структура ще
се считат за
парафазни.
Това решение
не
съответства
на приетите в
началото на
глава 3
предпоставки.
Тук то е
компромисно
и цели
по-бързо
осъществяване
на
изместванията
и
облекчаване
на микропрограмата
на
операцията.
Блок-схемата
на
микропрограмата
за изпълнение
на операция
деление на
числа с дясно
фиксирана
запетая,
представени
в прав код, в
показаната
по-горе
логическа
структура, е
представена
на
следващата
фигура 3.2.6.4.
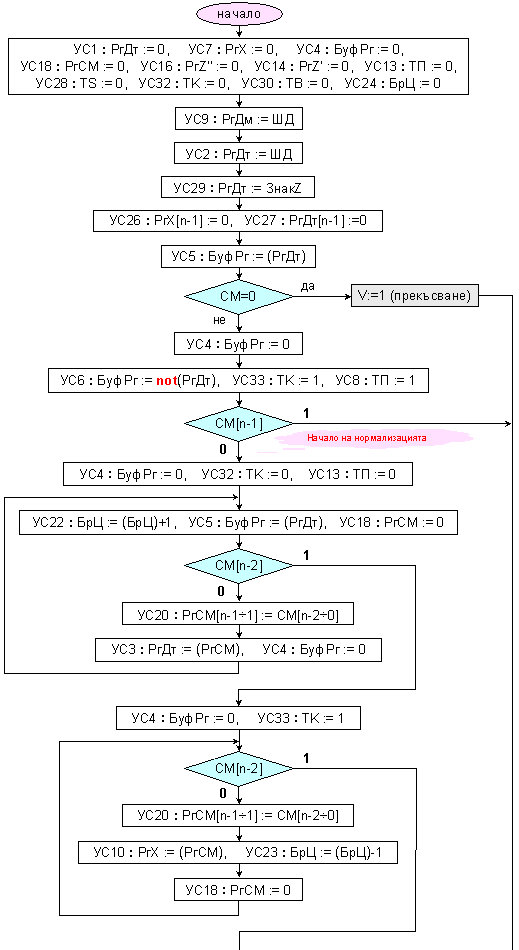
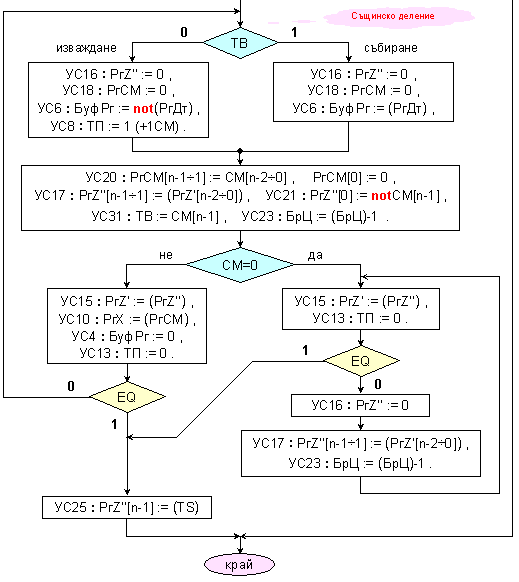
Фиг. 3.2.6.4.
Микропрограма
за деление на
числа с ДФЗ в
ПК без
възстановяване
на остатъка
в
устройство с
комбинационен
суматор, по
схемата с
неподвижен
делител
Микропрограмата на операция деление съдържа всички изброени по-горе етапи. Тя представлява по същество алгоритъм за деление без възстановяване на остатъка по модул, т.е. операндите в общия случай са числа със знак, представени в прав код. Този алгоритъм може да се използува и в случаите на деление на числа без знак. В нея обаче не са включени микрооперациите, свързани с определянето на остатъка. Тъй като определянето на остатъка Rx изисква многократно изместване на дясно, това изисква изграждане в логическата структура на коса връзка за дясно изместване на един бит. Последният частичен остатък, получен на изхода на суматора, както определя уравнение (3.2.6.10.б), следва да бъде изместван последователно през изходния регистър и регистъра на делимото, контролирано (k-l) пъти надясно. За целта може да се използва наличния в структурата брояч. Доработването на логическата структура и самия алгоритъм за тази цел оставяме на любознателния читател. Отново ще припомним, че в книга [2], в отделен раздел, той ще намери числени примери, които ще му помогнат да направи това.
Процесът
на деление в
логическата
структура от
фигура 3.2.6.3, който е
представен
чрез
блок-схемата
на микропрограмата
от фигура 3.2.6.4,
представлява
целочислено
деление, т.е.
получава се
цялата част
на частното.
Ако обаче
остатъкът от
делението е
различен от
нула,
процесът на
деление може
да продължи.
При това ще
се получават
все нови и
нови значещи
цифри, но те
ще формират
дробната
част на
частното
като реално
число.
Алгоритмично
лесно могат
да бъдат изчислени
още n
на брой цифри
за дробната
част, при
което частното
ще бъде
представено
във формат с
двойна
дължина. За
целта
основният
цикъл на същинското
деление
трябва да
бъде изпълнен
още веднъж,
до
следващото
(второ по ред)
нулиране на
брояча БрЦ.
Читателят следва да разбира, че операция деление е най-трудната и генерираща множество изключителни ситуации, ето защо изложеното по-горе съвсем не е достатъчно за пълното й изучаване. Тя, както и операция умножение вменяват на програмиста множество отговорности, ако той иска да получава верни и точни резултати. Още веднъж ще обърнем внимание на ситуацията “деление на нула”, която се характеризира с пълния консенсус между Конструктора и Програмиста за абсурдността и невъзможността изчислителният процес да продължи. Именно поради обезсмисляне на определението за смисъла на частното се мотивира решението за прекъсване и за канцелиране на програмата, в която тази ситуация е настъпила. По-късно в съответния раздел ще бъде обърнато внимание на това, че на прекъсването по тази причина е приписан най-висок приоритет и още, че то е определено като немаскируемо.
Следващият
раздел е:
3.2.7
Други методи
за деление (
Other methods for
division )