3.2.5.4 Умножение с два разряда едновременно
(със старшите разряди напред)

Multiplication with two bits at the same time (with the senior forward)

Ще представим алгоритъм за умножение с два разряда едновременно разработен за метода умножение със старшите разряди на множителя напред по схемата с неподвижно множимо. Този алгоритъм ще се основава на базовата логическа структура от фигура 3.2.4.1. Умножението на два разряда едновременно по метода със старшите разряди напред тук ще бъде разгледано за случая, когато съмножителите са представени в прав код, т.е. чрез модулите си, тъй като той е най-подходящ за излагане на принципите, които ще бъдат използувани.

И така, умножението започва с формиране на знака на произведението, който се запомня временно в тригера на знака, след което се нулират знаковите разряди на съмножителите. По този начин в логическата структура остават модулите на множимото и множителя. Същинското умножение започва с изместване на два разряда едновременно наляво, при което двата старши разряда на множителя (виж фигура 3.2.4.1) попадат в два допълнителни тригера, предварително поставени отляво на регистъра на множителя, в позиции с номера (n+1) и (n), където се подлагат на анализ. В двойката разряди могат да попаднат четири комбинации: 00, 01, 10 и 11, което означава, че трябва да е възможно да бъдат формирани поразрядните произведения X.0, X.1, X.2 или X.3. Не всяко от тези произведения обаче се формира непосредствено и фактически. Част от тях се формират с излишък с помощта на еднотипни микрооперации така, че да се получи една проста за корекция изчислителна схема на алгоритъма. Назначените за четирите комбинации операции са представени в следната таблица:

Таблица 3.2.5.4.1 Определяне на операцията

		операция	Необходима ли е корекция ?
0	0	+0	НЕ - правилно формирана междинна сума
0	1	+2.X	ДА - межд. сума е формирана с излишък +X
1	0	+2.X	НЕ - правилно формирана междинна сума
1	1	+4.X	ДА - межд. сума е формирана с излишък +X

Очевидно е, че в случаите, когато двойката разряди (y_i , y_i-1) на множителя представлява четно число (0 и 2), междинната сума е вярна, а когато представлява нечетно число (1 и 3), тя е формирана с излишък (съдържа един път множимото в повече). Естествено този излишък представлява грешка и трябва да бъде отнет от междинната сума, което обаче не е възможно да стане в текущия такт, ето защо се отлага във времето, т.е. за следващия такт. Междувременно обаче, след изместването на междинната сума наляво на два разряда в началото на следващия такт, натрупаният излишък (+Х) увеличава теглото си по отношение на неподвижното множимо четири пъти и ще има теглото (+4Х).

След изместването на междинната сума и множителя следва за пореден път да се определи текущата операция. За целта се анализира новата двойка разряди на множителя. Това обаче не е достатъчно, тъй като са възможни описаните вече задължения от предходния такт. Така за определяне на резултантната операция е необходимо да се разпознае необходимостта от корекция, поради вероятността от неправилно формиране в предходния такт на междинна сума. Така за целта на това разпознаване се налага да бъде въведена специална логическа функция на корекцията, чиито логически стойности се определят в зависимост от смисъла на четвъртата колонка в таблица 3.2.5.4.1. Интерпретирайки тази таблица като таблица на истинност лесно синтезираме аналитичния вид на логическата функция на корекцията:

Получената зависимост по същество означава, че за разпознаване на необходимостта от корекция на натрупаната междинна сума може да се използва младшият разряд на предидущата двойка, с която вече е било извършено умножение. Тъй като в алгоритмите за умножение по метода със старшите разряди напред изместването предхожда събирането, реализацията на тази логическа функция представлява просто още един тригер вляво на регистъра на множителя, в позиция с номер (n+2). И трите допълнителни тригера за цифрите на множителя (y_i+1 , y_i , y_i-1) практически са свързани с веригата за изместване на 2 разряда наляво, а тяхното начално съдържание е необходимо да бъде нула.

Според изложеното, на всеки такт от алгоритъма за умножение, с междинната сума се извършва операция, която се определя от трите текущи цифри на множителя, попаднали след направеното изместване на 2 разряда в допълнителните позиции (n+2, n+1, n) на регистъра на множителя. Обобщените резултантни операции, които могат да бъдат назначени във всеки отделен такт, са представени в следващата таблица.

Таблица 3.2.5.4.2 Определяне на опрацията

			операция
0	0	0	+0	0
0	0	1	+2.X	1
0	1	0	+2.X	0
0	1	1	+4.X	1
1	0	0	+0 - 4.X = -4.X	0
1	0	1	+2.X - 4.X = -2.X	1
1	1	0	+2.X - 4.X = -2.X	0
1	1	1	+4.X - 4.X = +0	1

Веднага може да се забележи еквивалентността на стойностите на функцията за корекция K^(t) и цифрите на младшия разряд y_i-1 на текущата двойка разряди от множителя. Така, поставената в първата колонка цифра y_i+1 трябва да интерпретираме като функция за корекция. Тогава излиза, че в първата половина на горната таблица са операции, които не се коригират, а във втората половина са операции, които се коригират. Резултантните операции се получават като сума от операцията, определена от текущата двойката разряди на множителя (y_i , y_i-1) и теглото на корекцията (-4.X), признак за която е цифрата (y_i+1=1).

Допълнително внимание заслужава последният такт на алгоритъма, когато след изместване наляво на два разряда, се извършва умножение с най-младшите два разряда на множителя (y₁ , y₀). Според изведените по-горе правила това умножение не винаги е точно. В случаите, когато младшата цифра на двойката разряди е единица y₀=1, в междинната сума се натрупва множимото един път в повече, т.е. въпреки, че умножението завършва, произведението не е вярно. В тези случаи умножението трябва да завърши с изваждане на излишъка от получената сума за да се формира вярно произведение. Необходимостта от тази корекция се установява след последното изместване само на множителя, при което най-младшата му цифра (нулевият разряд) попада в позиция (n+2), където стойността й ще бъде анализирана в качеството й на признак за корекция.

Умножението завършва със запис на знака на произведението, взет от тригера на знака TS.

И така, при числа представени в прав код, алгоритъмът за умножение на 2 разряда едновременно със старшите разряди напред, може да бъде реализиран в базовата логическа структура, представена на фигура 3.2.4.1, която е построена по схемата с неподвижно множимо. Измененията, които трябва да се извършат в тази структура, са следните:

- необходимо е да се изградят връзки за еднотактно изместване на два разряда наляво;

- необходими са три допълнителни разряда в изместващия регистър на множителя;

- старшата половина на суматора трябва да бъде пълноценна;

- необходимо е да се изградят връзки за изместване на множимото на 1 и на 2 разряда за получаване на поразрядните произведения 2.X и 4.X.

Както се вижда от таблица 3.2.5.4.2, описаният алгоритъм за умножение изисква изпълнение на операция събиране и операция изваждане. За правилното изпълнение на операция изваждане обаче е необходимо в схемата с неподвижно множимо, последното да се подава към суматор с двойна дължина. Операция (-2.X) например изисква изпълнение по следната схема:

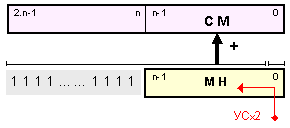
Фиг. 3.2.5.4.1. Схема за реализация на операция изваждане (-2.Х) в суматор с двойна дължина

а операция (-4.Х) изисква изпълнение по следната схема:

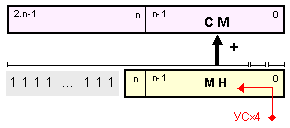
Фиг. 3.2.5.4.2. Схема за реализация на операция изваждане (-4.Х) в суматор с двойна дължина

И в двете схеми множимото се подава изместено наляво на един или на два разряда, което се постига с отделни управляващи сигнали. Тъй като при изваждане умалителят се подава към суматора в обратен код, то въведените отляво незначещи цифри са единици, т.е. логическите връзки на изхода регистъра на множимото са както прави така и инверсни, при това коси на 1 и на 2 разряда. Това налага старшата половина на суматора да се реализира като пълноценна, т.е. тя не предлага възможностите за облекчаване, които бяха реализирани в логическата структура от фигура 3.2.4.1.

Представения алгоритъм е илюстриран с подходящо подбрани примери в книга [2].

След последните пояснения става очевидно значителното усложнение на логическата структура, реализираща изложения тук алгоритъм, по сравнение с тази, в която умножението се изпълнява последователно и само с един разряд на множителя.

Изложеният алгоритъм може да бъде модифициран и за случая, когато операндите са представени в допълнителен код. В този случай схемата с неподвижно множимо изисква алгоритъмът да започне с корекция на псевдопроизведението, ако множителят е отрицателен, тъй като в края на умножението, множимото се намира според тази схема, под младшите разряди на псевдопроизведението и тогава нейната реализация няма да бъде еднотактна микрооперация. Разработването и изследването на този алгоритъм оставяме на читателя.

Алгоритъмът за умножение на два разряда едновременно със старшите напред е известен още като алгоритъм на Мак’Сорли (Mac'Sorley) - предложен през 1961 год.

Следващият раздел е:

3.2.5.5 Алгоритъм на Мак’Сорли ( Algorithm of Mac'Sorley )