1.6.5
Обратен код
Ones
complement representation
Сравнявайки
определението
(1.6.2.10) със
схемата (1.6.4.5)
може да се
установи, че
те са еднакви
по форма.
Обобщавайки
случаите на числа
с
положителен
и
отрицателен
знак и придавайки
на
умаляемото в
разликата (1.6.4.5)
смисъл на модул
за
сравнимост,
може да
запишем
следната
форма:
![]()
където в
общия случай
![]()
Полученото
може да се
разглежда
като изобразяващ
код, тъй като
определението
му съвпада с
вида на
определението
(1.6.2.10).
Получаването
на обратния
код на
числото X става по
начина,
описан в
предидущия
пункт. Когато
числото е
двоично,
изпълнението
на горното
определение
се постига по
схемата (1.6.4.7), което
дава
основание
кодът да се
нарече обратен.
И тук фактическата
операция
изваждане в
определението
се подменя с
логическо
поразрядно
инвертиране
на
съдържащите
се в разрядната
мрежа цифри.
Така определението
на обратния
код за
двоични числа
приема
следната
конкретна
форма:
![]()
която се основава на формата за прав код (1.6.1.3).
Следва
да обърнем
внимание на
отношението
на модулите
за
сравнимост в
двата кода, т.е.
че Q<M. Това
означава, че
в случаите на
изобразяване
по модул Q в
изобразяващата
област на
разрядната
мрежа L, правата
задача за
сравнимост
има
неединствено
решение за някои
числа.
Аналогично
на случаите в
прав код и
тук този факт
се отнася за
числото нула,
като се
различават
две кодови
комбинации
за двете
знакови нули:
+0 и 0, съответно:
![]()
Ето
защо и двата
случая в
определението
(1.6.5.2) съдържат
знак за
равенство.
Пълното
съответствие
на кодовите
комбинации е
представено
в таблица 1.6.5.1.
Таблица
1.6.5.1
Кодово
съответствие
|
комбинация |
число |
|
000 ...
000 |
+0 |
|
000 ...
001 |
+1.d |
|
000 ...
010 |
+2.d |
|
000 ...
011 |
+3.d |
|
-
- - - - - - - - |
-
- - - - - |
|
011 ...
111 |
|
|
100 ...
000 |
|
|
-
- - - - - - - - |
-
- - - - - |
|
111 ...
101 |
-2.d |
|
111 ...
110 |
-1.d |
|
111 ...
111 |
-0 |
От
кодовата
таблица на
обратния код
може да се
направи
извод, че
диапазонът
на представимите
в този код
числа е
напълно симетричен
и съвпадащ с
диапазона на
числата в
прав код.
Връщайки се към казаното в предидущия пункт, можем да дадем още една полезна форма на определението за допълнителен код:
![]()
Получаването
на
модифициран
обратен код е
аналогично
на
получаването
на модифициран
допълнителен
код, т.е. чрез
добавяне на още
един знаков
разряд в
разрядната
мрежа.
И този код притежава цикличната зависимост:
![]()
което
означава, че
всевъзможните
преобразувания
на кодовете
(прав,
обратен,
допълнителен)
могат да се
извършват с
помощта на един
единствен
алгоритъм.
След всичко казано до момента, окончателно можем да заявим, че задачата за синтез на алгоритъм за преход от естествен вид на числата към изображението им в допълнителен код и обратно е решена. Този алгоритъм е следния:
1. Даденото
число се
представя в
двоична бройна
система и се
записва в
разрядната
мрежа под
формата на
прав код
знак и модул
на числото,
според (1.6.1.3), т.е.
![]()
2. Анализира
се
съдържанието
на знаковия
бит на
разрядната
мрежа xn-1=?:
·
Ако
заковият бит
съдържа нула,
т.е. числото е
положително,
тогава
![]()
Следва
преход в
пункт 3.
·
Ако
заковият бит
съдържа
единица, т.е.
числото е
отрицателно,
тогава:
а)
според (1.6.5.2) се
получава
обратния код на
числото:
![]()
б)
според (1.6.5.3) се
получава
допълнителния
код на
числото:
![]()
3.
Край.
При
изпълнение
на операция
събиране или
изваждане,
може да се
работи с
кодовите
комбинации,
изобразяващи
операндите,
т.е. с техните
обратни
кодове.
Събирането
се извършва в
n-разряден
суматор като
аритметическа
операция, а
получената
кодова сума
следва да се
интерпретира
като код на
резултата.
Както за
допълнителния
код, така и в
този случай,
може да се
докаже
твърдението,
че
![]()
ако при
събирането
не е
настъпило
препълване
на диапазона
на
представимите
в този код
числа. Това
твърдение се
основава на
теорема (1.6.2.15).
Доказателството
му оставяме
на читателя,
но някои
особености
на този код,
които трябва
да се имат
предвид, ще
изясним. Така
например, при
събиране на
кодови
комбинации
от втората
половина на
кодовата
таблица 1.6.5.1,
настъпва
препълване
на
разрядната
мрежа. Теглото
на
възникващия
при това
пренос от най-старшия
бит всъщност
е равно на
модула на
разрядната
мрежа, т.е. при
двоичен код:
![]()
В тази
ситуация в
разрядната
мрежа остава разликата
между
кодовата
сума S
и модула на
разрядната
мрежа, т.е. в
разрядната
мрежа остава
числото (S-N).
Според
схемата за
работа в
допълнителен
код, с това се
постига
привеждане
на сумата в
изобразяващата
област, тъй
като модулът
на
разрядната
мрежа
съвпада с
модула на кода
(вижте фигура
1.6.2.4).
В
условията на
обратен код
обаче,
модулът на
разрядната
мрежа N не
съвпада с
модула на
кода Q. Ако
при събиране
на две кодови
комбинации възникне
пренос от
най-старшия
разряд, оставащата
в разрядната
мрежа кодова
комбинация
няма да бъде
сравнима по
модул Q
с истинската
сума. Като се
има предвид
връзката
между N и Q, а
именно, че Q=N-1,
става ясно,
че преносът
от
разрядната
мрежа отнася
от
оставащата в
нея младша
част на сумата
една единица
в повече. За
да бъде оставащата
в разрядната
мрежа
комбинация
сравнима по
модул Q, то
нанесената й
щета следва
да бъде
възстановена,
което може да
се постигне
лесно чрез прибавяне
на единица в
младшия
разряд. Тъй като
такава
корекция е
необходимо
да се извършва
винаги,
когато
възникне
пренос от
най-старшия
разряд, тя се
постига чрез
връзката
![]()
Свързването
в суматора на
най-старшия
пренос с
най-младшия
се нарича циклически
пренос при
обратен код.
Това решение
е показано на
следната
рисунка
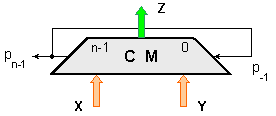
Фиг. 1.15.
Двоичен
комбинационен
суматор с циклически
пренос
Операция изваждане се свежда по описания вече начин към операция събиране чрез смяна на знака на умалителя, т.е. X-Y=X+(-Y).
Последното, което трябва да бъде изяснено, е как ще се открива препълване на диапазона на представимите в обратен код числа. Признаците за разпознаване на препълването се изявяват в процеса на доказване на твърдението (1.6.5.5) или аналогичното му за случая на събиране в модифициран обратен код. Без да привеждаме тези доказателства тук, ще твърдим, че функциите (1.6.2.18), (1.6.2.19) и (1.6.3.2) са същите, с което ще приемем, че те влизат в сила и при обратен код.
В
заключение
се налага
изводът, че представянето
на числата в
допълнителен
(или в
обратен код,
както и в
модифицирани
такива), е за
предпочитане,
тъй като тяхното
събиране и
изваждане се
извършва директно върху
кодовите
комбинации,
резултатът
се получава
автоматично
в същия код, в
който са
операндите.
За това е
необходим
само n-разряден
двоичен
суматор.
Следователно,
от гледна
точка на
оперирането
с числата (имаме
предвид
както
операндите,
така и всички
междинни и
окончателни
резултати), е
най-удобно
същите да се
съхраняват в
паметта на
компютъра
като
представени
в допълнителен
код.
Множество
числени
примери,
илюстриращи
казаното,
читателят ще
намери в книга
[2].
Следващият
раздел е:
1.6.6
Двоично-десетични
кодове
( Binary Decimal
Codes )